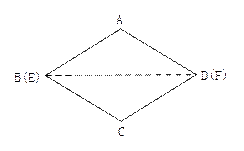
如图①，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起
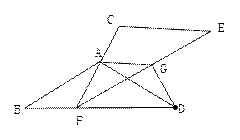
（1）操作：如图②，将△ECF的顶点F固定在△ABD的BD边上的中点处，将△ECF绕点F在BD的上方左右旋转，设旋转时FC交BA于H（不与点B重合），EF交DA于G（不与点D重合），求证：BH·GD=BF2
（2）操作：如图③，△ECF的顶点F在△ABD的BD边上滑动（不与点B、D重合），且CF如终过点A，过点A作AG∥CE，交EF于G，连接DG
探究：FD+DG= ，并请证明你的结论
 |
|||||
 |
|||||
 |
|||||
已知如图，二次函数y=ax2 +bx+c的图像过A、B、C三点
(1)观察图像写出A、B、C三点的坐标
(2)求出二次函数的解析式
已知二次函数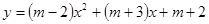
的图象过点（0， 5）
⑴ 求m的值，并写出二次函数的关系式；
⑵ 求出二次函数图象的顶点坐标、对称轴．
已知二次函数y=-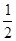
x2 –x+4回答下列问题
（1）用配方法将其化成y="a" (x-h)2+k的形式
（2）指出抛物线的顶点坐标和对称轴
（3）当x取何值时，y随x增大而增大; 当x取何值时，y随x增大而减小？
二次函数过A(-1,0) B(0,-3)两点，且对称轴是X=1求出它的解析式
如图，在方格纸上，分别过A画AD的垂线、过B画EF的垂线、过C画GF的垂线.