九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践——应用——探究的过程
(1)实践:他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量,测得隧道的路面宽为10米,隧道顶部最高处距地面6.25米,并画出了隧道截面图,建立了如图所示的直角坐标系,请你求出抛物线的解析式
(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖起方向上的高度差至少为0.5米,为了确保安全,问该隧道能否让最宽3米,最高3.5米的两辆车居中并列行驶(不考虑两车之间的空隙)?
(3)探究:该课题学习小组为进一步探究抛物线的有关知识,他们借助上述抛物线模型,提出了以下两个问题,请予解答:
①如图,在抛物线内作矩形ABCD,使顶点C、D落在抛物线上,顶点A、B落在x轴上,设矩形ABCD的周长为为l,求l的最大值
②如图,过原点作一条直线y=x,交抛物线于M,交抛物线的对称轴于N,P为直线OM上一动点,过点P作x轴的垂线交抛物线于点Q,问在直线OM上是否存在点P,使以点P、N、Q为顶点的三角形为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由
 |
(本题满分10分,其中第(1)小题6分,第(2)小题4分)
如图,已知在△ABC中,点D在边AC上,CD∶AD=1∶2,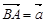 ,
,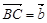 .
.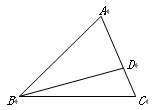
(1)试用向量
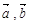 表示向量
表示向量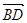 ;
;(2)求作:
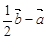 .(不要求写作法,但要指出所作
.(不要求写作法,但要指出所作
图中表示结论的向量)
(本题满分10分,其中第(1)小题4分,第(2)小题6分)
已知抛物线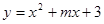 的对称轴为x=-2.
的对称轴为x=-2.(1)求m的值;
(2)如果将此抛物线向右平移5个单位后,求所得抛物线与y轴的交点坐标.
如图,在△ABC中,已知AB=AC,∠BAC=90o,BC=6cm,,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连结AD、AE,设运动时间为t秒.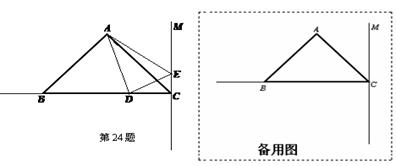
(1)求AB的长;
(2)当t为多少时,△ABD的面积为6
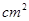 ?
?(3)当t为多少时,△ABD≌△ACE,并简要说明理由(可在备用图中画出具体图形).
已知:如图,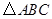 中,
中,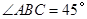 ,
,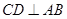 于
于 ,
,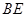 平分
平分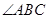 ,且
,且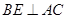 于
于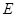 ,与
,与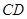 相交于点
相交于点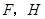 是
是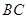 边的中点,连结
边的中点,连结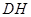 与
与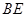 相交于点
相交于点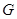 .
.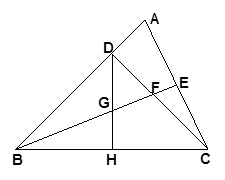
(1)说明:
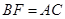 ;
;(2)说明:
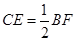 ;
;(3)试探索
 ,
,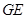 ,
,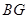 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
某超市决定从厂家购进甲、乙、丙三种不同型号的计算器80只,其中甲种计算器的只数是乙种计算器只数的2倍,购买三种计算器的总金额不超过3300元.已知甲、乙、丙三种计算器的出厂价格分别为:30元/只、40元/只、50元/只.(1)至少购进乙种计算器多少只?
(2)若要求甲种计算器的只数不超过丙种计算器的只数,则有哪些购买方案?