已知:如图,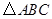 中,
中,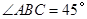 ,
,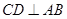 于
于 ,
,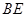 平分
平分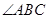 ,且
,且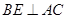 于
于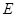 ,与
,与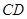 相交于点
相交于点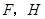 是
是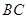 边的中点,连结
边的中点,连结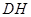 与
与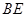 相交于点
相交于点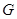 .
.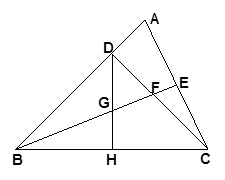
(1)说明:
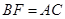 ;
;(2)说明:
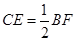 ;
;(3)试探索
 ,
,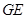 ,
,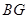 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
解方程:
计算:72°35′÷2 + 18°33′×4
计算:
如图,将一张正方形纸片剪成四个小正方形,如图(1);然后再将其中的一个正方形剪成四个小正方形,此时共有7个正方形,如图(2);再将其中的一个正方形剪成四个小正方形,此时共有10个正方形,如图(3).按此操作继续下去… ……
……
(1)根据以上操作方法,请你填写下表:
操作次数 |
1 |
2 |
3 |
4 |
5 |
… |
| 正方形的个数S |
4 |
7 |
10 |
… |
(2)用代数式表示正方形的个数S和操作次数 之间的关系;
之间的关系; (3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.
(3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.
某检修站,工人乘一辆汽车沿东西方向的公路检修线路,约定向东为正,向西为负,从A地出发到收工时,行走记录为(单位:千米):
+15,-2,+5,-1,+10,-3,-2,-12,+4,-5,+6
(1)计算收工时,工人在A地的哪一边,距A地多远?
(2)若汽车每行驶100千米耗油8升,求这一天汽车共耗油多少升?