若点P'(m,-1)是点P(2,n)关于x轴的对称点,求m+n
已知点P(x,y)在第四象限,它到x轴的距离为2,到y轴的距离为3,求P点的坐标
将一长方形纸片按如图的方式折叠,BC、BD为折痕,求∠CBD的度数
我们知道两条直线相交,一共有两对对顶角、4对邻补角,那么三条直线、四条直线,甚至是几条直线交于一点或两两相交有多少对对顶角和邻补角?请动手操作,观察填表,并归纳。

 ……
……
① ② ③
(1)请观察上图并填写下表:
| 图形编号 |
① |
② |
③ |
…… |
| 对顶角的对数 |
2 |
6 |
12 |
|
| 邻补角的对数 |
4 |
12 |
24 |
(2)若n条直线相交于一点,则共有多少对对顶角?共有多少对邻补角?
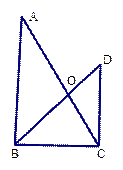
数学课上,老师挂出小黑板,两个三角板按如图所示的位置放置。图中有对顶角和邻补角?请你把图中所有的对顶角和邻补角都写出来。