（本题6分）博才中学要从甲、乙两名同学中选拔一名同学代表学校参加“华罗庚金杯”数学竞赛活动。这两位活动同学最近四次的数学测验成绩如下表：（单位：分）
| |
第一次 |
第二次 |
第三次 |
第四次 |
| 甲 |
75 |
70 |
85 |
90 |
| 乙 |
85 |
82 |
75 |
78 |
（1）根据表中数据,分别求出甲、乙两名同学这四次数学测验成绩的平均分.
(2)经计算,甲、乙两位同学这四
次数学测验成绩的方差分别为
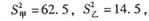你认为哪位同学的成绩较稳定?请说明理由.
若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-
，x1•x2=
．把它称为一元二次方程根与系数关系定理．如果设二次函数y=ax2+bx+c（a≠0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．利用根与系数关系定理可以得到A、B两个交点间的距离为：AB=|x1-x2|=
；
参考以上定理和结论，解答下列问题：
设二次函数y=ax2+bx+c（a＞0）的图象与x轴的两个交点A（x1，0），B（x2，0），抛物线的顶点为C，显然△ABC为等腰三角形．
（1）当△ABC为直角三角形时，求b2-4ac的值；
（2）当△ABC为等边三角形时，求b2-4ac的值．
在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上．
（1）从A、D、E、F四点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是等腰三角形的概率是 ．
（2）从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率．（用树状图或列表法求解）
某班班委主动为班上一位生病住院的同学筹集部分医药费，计划筹集450元，由全体班委同学分担，有5名同学闻讯后也自愿参加捐助，和班委同学一起平均分担，因此每个班委同学比原先少分担45元，问：该班班委有几个？
如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D=2∠CAD．
（1）求∠D的度数；
（2）若CD=1，求BD的长．
求证：圆的内接四边形对角互补．