(本题20分) (湖南湘西,25,20分)如图.抛物线 与x轴相交于点A和点B,与y轴交于点C.
与x轴相交于点A和点B,与y轴交于点C.
(1)求点A、点B和点C的坐标.
(2)求直线AC的解析式.
(3)设点M是第二象限内抛物线上的一点,且 =6,求点M的坐标.
=6,求点M的坐标.
(4)若点P在线段BA上以每秒1个单位长度的速度从A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A 向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?
向C运动.设运动的时间为t秒,请求出△APQ的面积S与t的函数关系式,并求出当t为何值时, △APQ的面积最大,最大面积是多少?
如图.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,分别于BC、CD交于E、F,EH⊥AB于H.连接FH,求证:四边形CFHE是菱形.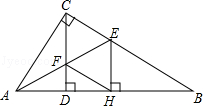
在水果店里,小李买了5kg苹果,3kg梨,老板少要2元,收了50元;老王买了11kg苹果,5kg梨,老板按九折收钱,收了90元,该店的苹果和梨的单价各是多少元?
先化简: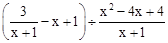 ,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
,然后从﹣1≤x≤2中选一个合适的整数作为x的值代入求值.
在矩形ABCD中,点P是边AD上的动点,连接BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连接QP(如图).已知AD=13,AB=5,设AP=x,BQ=y.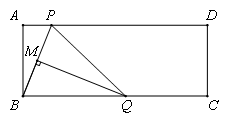
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,求x的值;
(3)点E在边CD上,过点E作直线QP的垂线,垂足为F,如果EF=EC=4,求x的值.
如图,在平面直角坐标系xOy中,顶点为M的抛物线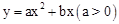 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.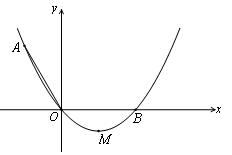
(1)求这条抛物线的表达式;
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.