在矩形ABCD中,点P是边AD上的动点,连接BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,连接QP(如图).已知AD=13,AB=5,设AP=x,BQ=y.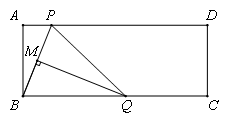
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,求x的值;
(3)点E在边CD上,过点E作直线QP的垂线,垂足为F,如果EF=EC=4,求x的值.
如图12所示的8×8网格中,每个小正方形边长均为1,以这些小正方形的顶点为顶点的三角形称为格点三角形在图12中以线段AB为一边,点P为顶点且面积为6的格点三角形共有个;

请你选择(1)中的一个点P为位似中心,在图12中画出格点△A′B′P,使
△ABP与△A′B′P的位似比为2:1求tan∠PB′A′的值.
计算: .
.
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为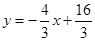 ,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4). 动点P从A点出发,在AB边上匀速运动. 动点Q从点B出发,在折线BCD上匀速运动,速度均为每秒1个单位长度. 当其中一个动点到达终点时,另一动点也停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
求出点C的坐标
求S随t变化的函数关系式;
当t为何值时,S有最大值?并求出这个最大值
有两张完全重合的矩形纸片,小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连结BD、MF,此时他测得BD=8cm,∠ADB=30°.
在图1中,请你判断直线FM和BD是否垂直?并证明你的结论;
小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;

若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少.
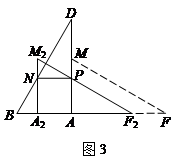
已知抛物线y=ax2+x+2.当a=-1时,求此抛物线的顶点坐标和对称轴
若代数式-x2+x+2的值为正整数,求x的值;
若a是负数时,当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0). 若点M在点N的左边,试比较a1与a2的大小.