有两张完全重合的矩形纸片，小亮将其中一张绕点A顺时针旋转90°后得到矩形AMEF（如图1），连结BD、MF，此时他测得BD＝8cm，∠ADB＝30°．
在图1中，请你判断直线FM和BD是否垂直？并证明你的结论；
小红同学用剪刀将△BCD与△MEF剪去，与小亮同学继续探究．他们将△ABD绕点A顺时针旋转得△AB1D1，AD1交FM于点K（如图2），设旋转角为β（0°＜β＜90°），当△AFK为等腰三角形时，请直接写出旋转角β的度数；
若将△AFM沿AB方向平移得到△A2F2M2（如图3），F2M2与AD交于点P，A2M2与BD交于点N，当NP∥AB时，求平移的距离是多少.
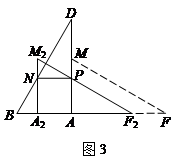
学习了统计知识后，王老师请班长就本班同学的上学方式进行了一次调查统计，图（1）和图（2）是班长和同学们通过收集和整理数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息，解答一下问题：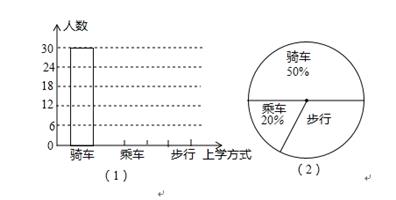
（1）计算出扇形统计图中“步行”部分所对应的圆心角的度数；
（2）求该班共有多少名学生；
（3）在图（1）中，将表示“乘车”与“步行”的部分补充完整．
如图，线段AD=18cm，线段AC=BD=12cm，E、F分别是线段AB、CD的中点，求线段EF的长．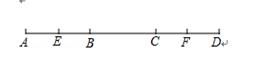
如图所示，∠AOB=∠AOC=90°，∠DOE=90°，OF平分∠AOD，∠AOE=36°．
（1）求∠COD的度数；
（2）求∠BOF的度数．
（1）计算：（﹣3）3÷2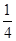
×（﹣
）2+4﹣22×（﹣
）．
（2）先化简，后求值：3a+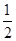
（a﹣2b）﹣（3a﹣6b），其中a=2，b=﹣3．
为了探究n条直线能把平面最多分成几部分，我们从最简单的情形入手：
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成11部分…；
把上述探究的结果进行整理，列表分析：
| 直线条数 |
把平面分成部分数 |
写成和形式 |
| 1 |
2 |
1+1 |
| 2 |
4 |
1+1+2 |
| 3 |
7 |
1+1+2+3 |
| 4 |
11 |
1+1+2+3+4 |
| … |
… |
… |
（1）当直线条数为5时，把平面最多分成部分，写成和的形式；
（2）当直线为n条时，把平面最多分成部分．