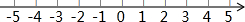(1)计算:(﹣3)3÷2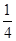 ×(﹣
×(﹣ )2+4﹣22×(﹣
)2+4﹣22×(﹣ ).
).
(2)先化简,后求值:3a+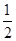 (a﹣2b)﹣
(a﹣2b)﹣ (3a﹣6b),其中a=2,b=﹣3.
(3a﹣6b),其中a=2,b=﹣3.
如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)(5分)求证:CG是⊙O的切线;
(2)(5分)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.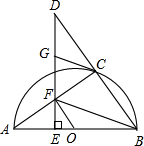
如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为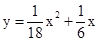
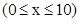 .发射3 s后,导弹到达A点,此时位于与L同一水平面的R处雷达站测得AR的距离是2 km,再过3s后,导弹到达B点.
.发射3 s后,导弹到达A点,此时位于与L同一水平面的R处雷达站测得AR的距离是2 km,再过3s后,导弹到达B点.
(1)(4分)求发射点L与雷达站R之间的距离;
(2)(4分)当导弹到达B点时,求雷达站测得的仰角(即∠BRL)的正切值.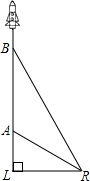
已知甲、乙两个班级各有50名学生.为了了解甲、乙两个班级学生解答选择题的能力状况,黄老师对某次考试中8道选择题的答题情况进行统计分析,得到统计表如下:
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 甲班 |
0 |
1 |
1 |
3 |
4 |
11 |
16 |
12 |
2 |
| 乙班 |
0 |
1 |
0 |
2 |
5 |
12 |
15 |
13 |
2 |
请根据以上信息解答下列问题:
(1)(2分)甲班学生答对的题数的众数是______;
(2)(2分)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=______(优秀率= ×100%).
×100%).
(3)(4分)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,则抽到的2人在同一个
班级的概率等于______.
如图,四边形ABCD是平行四边形,连接AC.
(1)(4分)请根据以下语句画图,并标上相应的字母(用黑色字迹的钢笔或签字笔画).
①过点A画AE⊥BC于点E;
②过点C画CF∥AE,交AD于点F;
(2)(4分)在完成(1)后的图形中(不再添加其它线段和字母),请你找出一对全等三角形,并予以证明.
已知三个一元一次不等式: ,
,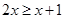 ,
, ,请从中选择你喜欢的两个不等式,组成一个不等式组,求出这个不等式组的解集,并把解集在数轴上表示出来.
,请从中选择你喜欢的两个不等式,组成一个不等式组,求出这个不等式组的解集,并把解集在数轴上表示出来.
(1)(2分)你组成的不等式组是
(2)(6分)解: