如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(1)(5分)求证:CG是⊙O的切线;
(2)(5分)若△AFB的面积是△DCG的面积的2倍,求证:OF∥BC.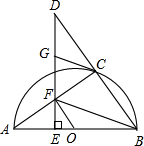
如图,一次函数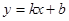 的图像与反比例函数
的图像与反比例函数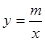 的图像交于
的图像交于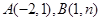 两点。
两点。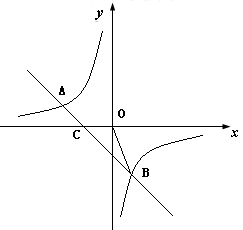
求:(1)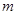 的值;
的值;
(2)求一次函数的解析式;
(3)若直线AB交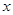 轴于点C,求△OBC的面积.
轴于点C,求△OBC的面积.
.一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分到达目的地.求前一小时的行驶速度.
如图,在反比例函数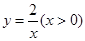 的图象上,有点
的图象上,有点 ,
,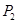 ,
, ,
,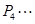 ,它们的横坐标依次为1,2,3,4
,它们的横坐标依次为1,2,3,4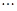 .分别过这些点作
.分别过这些点作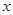 轴与
轴与 轴的垂线,图中所构成的阴影部分的面积从左到右依次为
轴的垂线,图中所构成的阴影部分的面积从左到右依次为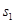 ,
,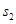 ,
,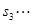
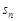 ,求:
,求:
(1) 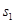 的值;
的值;
(2) 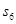 的值;
的值;
(3) 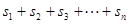 的值。(用含
的值。(用含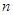 的代数式来表示)
的代数式来表示)
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题。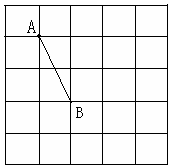
(1)图中线段AB的两端点都落在格点(即小正方形的顶点)上,求出AB的长度;
(2)再以AB为一边画一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;
(3)请直接写出符合(2)中条件的等腰三角形ABC的顶点C的个数.
先化简,再求值: (
( -2),其中x=2.
-2),其中x=2.