如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.
⑴说明四边形ACEF是平行四边形;
⑵当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.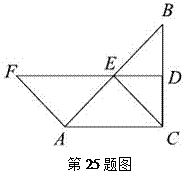
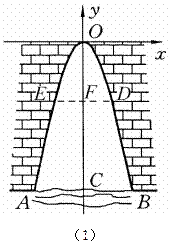
一个涵洞成抛物线形,它的截面如图(1).现测得,当水面宽AB =1.6 m时,涵洞顶点O与水面的距离为2.4 m.ED离水面的高FC="1.5" m,求涵洞ED宽是多少?是否会超过1 m?(提示:设涵洞所成抛物线为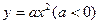 )
)
已知
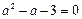 ,求代数式
,求代数式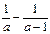 的值.
的值.
如图, 已知:BF=DE,∠1=2,∠3=∠4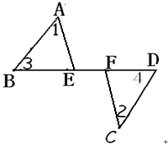
求证:AE=CF.
证明:
因式分解: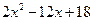
已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD. 探究下列问题:
(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD=;
(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD=;
(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相应的∠ACB的度数.


图1图2图3