已知:在△ABC中,BC=a,AC=b,以AB为边作等边三角形ABD. 探究下列问题:
(1)如图1,当点D与点C位于直线AB的两侧时,a=b=3,且∠ACB=60°,则CD= ;
(2)如图2,当点D与点C位于直线AB的同侧时,a=b=6,且∠ACB=90°,则CD= ;
(3)如图3,当∠ACB变化,且点D与点C位于直线AB的两侧时,求 CD的最大值及相应的∠ACB的度数.


图1 图2 图3
如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD,垂足为M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.

在“立德树人,志愿服务”活动月中,学校团委为了解本校学生一个月内参加志愿服务次数的情况,随机抽取了部分同学进行统计,并将统计结果分别分成A、B、C、D四类,根据统计结果绘制了如图所示的两幅不完整的统计图.

请根据图中信息解答下列问题:
(1)本次抽样调查了 名学生,并请补全条形统计图;
(2)被调查学生“一个月内参加志愿服务次数”的人数的众数落在 类.
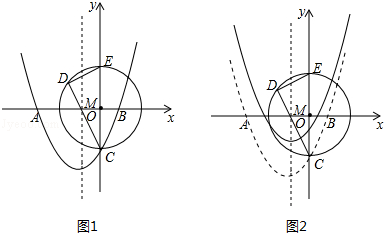
如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移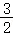 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 的长.

某水果商行计划购进A、B两种水果共200箱,这两种水果的进价、售价如下表所示:
|
价格 类型 |
进价(元/箱) |
售价(元/箱) |
|
A |
60 |
70 |
|
B |
40 |
55 |
(1)若该商行进贷款为1万元,则两种水果各购进多少箱?
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的 ,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?