在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A（﹣3，0）、B（1，
0），过顶点C作CH⊥x轴于点H．
（1）直接填写：a= ，b= ，顶点C的坐标为 ；
（2
）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标．
阅读下面材料：
问题：如图①，在△ABC中， D是BC边上的一点，若∠BAD=∠C=2∠DAC=45°，DC=2．求BD的长．
小明同学的解题思路是：利用轴对称，把△ADC进行翻折，再经过推理、计算使问题得到解决．
（1）请你回答：图中BD的长为；
（2）参考小明的思路，探究并解答问题：如图②，在△ABC中，D是BC边上的一点，若∠BAD=∠C=2∠DAC=30°，DC=2，求BD和AB的长．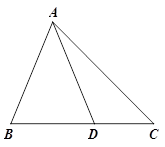
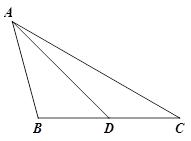
图①图②
在平面直角坐标系xOy中，一次函数y=k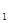
x+b与反比例函数y=
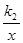的图象交于A(1,6)，B(a,3)两点.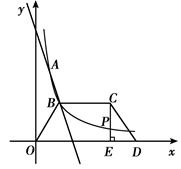
（1）求k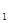，k
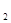的值；
（2）如图，点D在x轴上，在梯形OBCD中，BC∥OD,OB=DC,过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为18时，求PE：PC的值.
为了了解某校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成图1和图2尚不完整的统计图．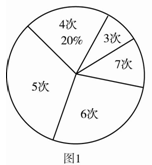
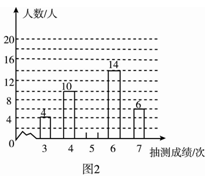
（1）本次抽测的男生有人，抽测成绩的众数是；
（2）请你将图2的统计图补充完整；
（3）若规定引体向上5次以上（含5次）为体能达标，则该校350名九年级男生中，估计有多少人体能达标？
已知:如图, BD是半圆O的直径,A是BD延长线上的一点，BC⊥AE，交AE的延长线于点C, 交半圆O于点E，且E为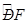
的中点.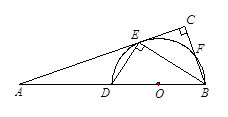 
（1）求证：AC是半圆O的切线；
（2）若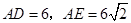
，求
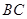的长．
如图，梯形ABCD中，AD∥BC，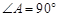
，BC=2，
，
．
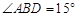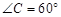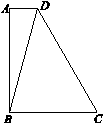
(1) 求∠BDC的度数； (2) 求AB的长．