如图，某广场设计的一建筑物造型的纵截面是抛物线的一部分，抛物线的顶点O落在水平面上，对称轴是水平线OC．点A、B在抛物线造型上，且点A到水平面的距离AC=4米，点B到水平面距离为2米，OC=8米．
（1）请建立适当的直角坐标系，求抛物线的函数解析式；
（2）为了安全美观，现需在水平线OC上找一点P，用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固，那么怎样才能找到两根支柱用料最省（支柱与地面、造型对接方式的用料多少问题暂不考虑）时的点P？（无需证明）
（3）为了施工方便，现需计算出点O、P之间的距离，那么两根支柱用料最省时点O、P之间的距离是多少？（请写出求解过程）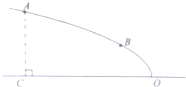
(本题满分14分)
如图，将一次函数
的图象上一点A(a，b)，沿竖直方向向上移动6个单位，得到点B，再沿水平方向向右移动8个单位，得到点C．以AC为直径作圆E，设垂直于y轴的直线DT与圆E相切于点D．
(1) 求证：点C在一次函数
的图象上；(2) 求三角形ADC的面积；
(3) 当点D在x轴上时，求点A的坐标．
(本题满分14分)(1) 如图所示的网格坐标系中，顶点在格点上的矩形ABCD被分割成四块全等的小矩形①、②、③、④，并经过一次或二次变换拼成正方形A1B1C1D1．试写出小矩形从①→⑤、③→⑦一种变换过程；
(2) 对任意一个矩形按(1)的方式实施分割、变换后拼成正方形．试探究矩形ABCD的周长与面积分别与正方形A1B1C1D1的周长与面积的大小关系？并用代数方法验证你的结论．
(本题满分14分)
如图是某市一条河上一座古拱挢的截面图，拱桥桥洞上沿是抛物线形状，抛物线拱桥处于正常水位时水面宽AB为26m，当水位上涨1m时，抛物线拱桥的水面宽CD为24m．现以水面AB所在直线为x轴，抛物线的对称轴为y轴建立直角坐标系．
(1) 求出抛物线的解析式；
(2) 经过测算，水面离拱桥顶端1.5m时为警戒水位．某次洪水到来时，小明用仪器测得水面宽为10m，请你帮助小明算一算，此时水面是否超过警戒水位．
(本题满分12分)已知AB是⊙O的一条弦，CD是⊙O的直径，CD⊥AB，垂足为K．现取一块三角板，把它的一个锐角顶点固定在点C处，该锐角的两边(从左到右)与直线AB和圆分别相交于E、F和G、H．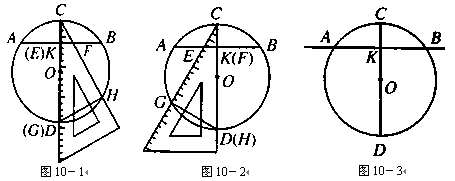
(1) 若∠C的一边过圆心，请选择图10-1或图10-2所示，求证： △CEF∽△CHG；
(2) 若∠C的边不过圆心，在图10-3中补全一种示意图，请你观察所画的图形，并判断(1)中的结论是否仍然成立？若成立，给予证明；若不成立，请说明理由．
(本题满分12分)
节假日，小明和哥哥在水族馆看完海洋动物后，参加了出口处的抽奖活动．游戏的规则如下：每张门票只可摸球一次，每次从装有大小形状相同的2个白球和1个红球的盒子中，随机摸出一个球，若摸出的是红球，则获得一份奖品．(1) 求每次摸球中奖的概率？
(2) 小明想：我有二张票，中奖的概率就翻一倍．你认为小明的思考正确吗？请用列表法或画树形图分析说明．