如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
(年山东德州12分)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.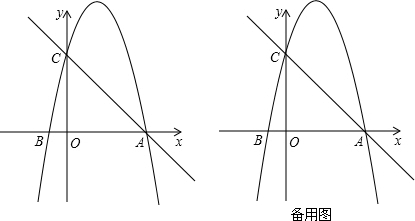
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作y轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
(年山东滨州12分)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.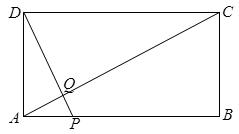
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
(年内蒙古呼和浩特12分)如图,已知直线l的解析式为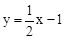 ,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D
,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D 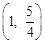 三点.
三点.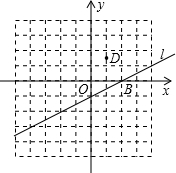
(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;
(2)已知点 P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E, 延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数, 并求出S的最大值及S最大时点P的坐标;
(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
(年辽宁营口14分)已知:抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),C(0,﹣3).
(1)求抛物线的表达式及顶点D的坐标;
(2)如图①,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线,交直线BC于点E.是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,请说明理由;
(3)如图②,过点A作y轴的平行线,交直线BC于点F,连接DA、DB.四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点B重合时立即停止运动.设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S,请求出S与t的函数关系式.
(2014年辽宁阜新12分)如图,抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,已知经过点A,B的直线的表达式为y=x+3.
(1)求抛物线的函数表达式及其顶点C的坐标;
(2)如图①,点P(m,0)是线段AO上的一个动点,其中-3<m<0,作直线DP⊥x轴,交直线AB于D,交抛物线于E,作EF∥x轴,交直线AB于点F,四边形DEFG为矩形.设矩形DEFG的周长为L,写出L与m的函数关系式,并求m为何值时周长L最大;
(3)如图②,在抛物线的对称轴上是否存在点Q,使点A,B,Q构成的三角形是以AB为腰的等腰三角形?若存在,直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.