已知直线y= x+4
x+4 与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
与x轴、y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
(1)试确定直线BC的解析式.
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
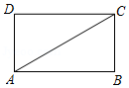
如图,四边形 是矩形.
(1)用尺规作线段 的垂直平分线,交 于点 ,交 于点 (不写作法,保留作图痕迹);
(2)若 , ,求 的长.
先化简,再求值: ,其中 .
解不等式组:
已知抛物线 经过点 、 ,与 轴交于点 .
(1)求这条抛物线的解析式;
(2)如图1,点 是第三象限内抛物线上的一个动点,当四边形 的面积最大时,求点 的坐标;
(3)如图2,线段 的垂直平分线交 轴于点 ,垂足为 , 为抛物线的顶点,在直线 上是否存在一点 ,使 的周长最小?若存在,求出点 的坐标;若不存在,请说明理由.

如图1,在 中, , , ,点 、 分别是边 、 的中点,连接 .将 绕点 逆时针方向旋转,记旋转角为 .
(1)问题发现
①当 时, ;
②当 时, .
(2)拓展探究
试判断:当 时, 的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
绕点 逆时针旋转至 、 、 三点在同一条直线上时,求线段 的长.
