已知抛物线yax2bx4经过点A(2,0)、B(4,0)，与-优题课

题文

已知抛物线 $y = a x^{2} + bx - 4$ 经过点 $A (2, 0)$ 、 $B (- 4, 0)$ ，与 $y$ 轴交于点 $C$ ．

（1）求这条抛物线的解析式；

（2）如图1，点 $P$ 是第三象限内抛物线上的一个动点，当四边形 $ABPC$ 的面积最大时，求点 $P$ 的坐标；

（3）如图2，线段 $AC$ 的垂直平分线交 $x$ 轴于点 $E$ ，垂足为 $D$ ， $M$ 为抛物线的顶点，在直线 $DE$ 上是否存在一点 $G$ ，使 $ΔCMG$ 的周长最小？若存在，求出点 $G$ 的坐标；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数的最值待定系数法求二次函数解析式相似三角形的判定与性质待定系数法求一次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

（1）在左图所示编号为①、②、③、④的四个三角形中，关于y轴对称的两个三角形的编号为　　　　　　　　；（2）在右图中，画出与△ABC关于x轴对称的△A₁B₁C₁_。

(1)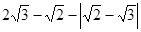（2）

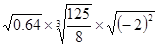
把一副三角板按如图甲放置，其中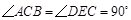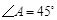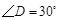，，，斜边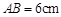，．把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙）．这时AB与CD₁相交于点、与D₁E₁相交于点F．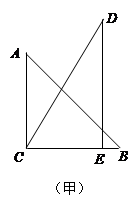

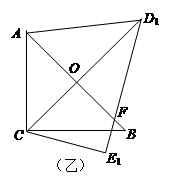
（1）求的度数；
（2）求线段AD₁的长；
（3）若把三角形D₁CE₁绕着点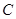顺时针再旋转30°得△D₂CE₂，这时点B在△D₂CE₂的内部、外部、还是边上？请说明理由。

为美化萧山，创建文明城市．园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个，摆放在人民广场两侧，搭配每个造型所需花卉情况如下表所示：

造型	甲	乙
A	90盆	30盆
B	40盆	100盆

综合上述信息，解答下列问题：
（1）符合题意的搭配方案有哪几种？
（2）若搭配一个A型造型的成本为1000元，
搭配一个B型造型的成本为1200元．试说明运用（1）中哪种方案成本最低？

我市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛，他们的成绩（单位：cm）如下：
甲：170 165 168 169 172 173 168 167
乙：160 173 172 161 162 171 170 175
（1）甲、乙两名运动员的跳高平均成绩分别是多少？
（2）哪名运动员的成绩更为稳定？为什么？
（3）若预测，跳过165cm就很可能获得冠军。该校为了获得冠军，可能选哪位运动员参赛？若预测跳过170cm才能得冠军呢？

试卷网试题网古诗词网作文网范文网