如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
(1)求证:△MDC是等边三角形;
(2)将△MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,点E,F和点A构成△AEF.试探究△AEF的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△AEF周长的最小值.
如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

如图,已知EC∥AB,∠EDA=∠ABF.
(1)求证:四边形ABCD是平行四边形;
(2)求证:OA2=OE•OF.

如图,函数y1=﹣x+4的图象与函数 的图象交于A(m,1),B(1,n)两点.
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,y1和y2的大小关系.

2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图.
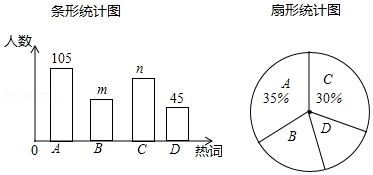
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数 的图象上的概率.