如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力)。
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置。
(2)在电场I区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置。
(3)若将左侧电场II整体水平向右移动L/n(n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场I区域内由静止释放电子的所有位置。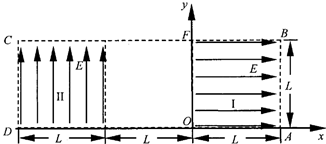
如图所示,质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点,水平轻质弹簧一端栓在固定挡板P上,另一端与靶盒A连接。Q处有一固定的发射器B,它可以瞄准靶盒发射一颗水平速度为v0=50m/s,质量m=0.010kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短。不计空气阻力。求弹丸进入靶盒A后,弹簧的最大弹性势能为多少?
如图所示,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h。一质量为m的子弹以水平速度v0射入物块后,以水平速度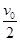 射出.已知重力加速度为g,求:
射出.已知重力加速度为g,求:
(1)此过程中系统损失的机械能。
(2)此后物块落地点离桌面边缘的水平距离。
某小型实验水电站输出功率是20kW,输电线路总电阻是6Ω.
(1)若采用380V输电,求输电线路损耗的功率.
(2)若改用5000V高压输电,用户端利用n1:n2=22:1的变压器降压,求用户得到的电压.
质量m1=10g的小球在光滑的水平桌面上以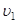 =30cm/s的速率向右运动,恰好遇上在同一条直线上向左运动的另一个小球.第二个小球的质量为m2=50g,速率
=30cm/s的速率向右运动,恰好遇上在同一条直线上向左运动的另一个小球.第二个小球的质量为m2=50g,速率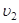 =10cm/s.碰撞后,小球m2恰好停止.那么,碰撞后小球m1的速度是多大,方向如何?
=10cm/s.碰撞后,小球m2恰好停止.那么,碰撞后小球m1的速度是多大,方向如何?
如图所示,光滑水平面上放有A、B、C三个物块,其质量分别为mA=2.0kg,mB=mC=1.0kg,用一轻弹簧固接A、B两物块,B、C只是靠在一起.现用力压缩弹簧使三物块靠近,此过程外力做功72J,然后释放,求:
(1)释放后物块B对物块C一共做了多少功?
(2)弹簧第二次被压缩时,弹簧具有的最大弹性势能为多大?