如图所示,一质量为M的物块静止在桌面边缘,桌面离水平地面的高度为h。一质量为m的子弹以水平速度v0射入物块后,以水平速度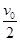 射出.已知重力加速度为g,求:
射出.已知重力加速度为g,求:
(1)此过程中系统损失的机械能。
(2)此后物块落地点离桌面边缘的水平距离。
宇航员 在太空中沿直线从A点运动到B点,他的运动图像如图所示,图中v是宇航员的速度,x是他的坐标。求:
在太空中沿直线从A点运动到B点,他的运动图像如图所示,图中v是宇航员的速度,x是他的坐标。求:
(1)宇航员从A点运动到B点所需时间。
(2)若宇航员以及推进器等装备的总质量恒为240kg,从A点到B点的过程中宇航员身上背着的推进器做功所消耗的能量为多少?
如图所示,A、B、C、D分别为p-V图中矩形的顶点,其中AB、CD为等容线,BD、AC为等压线。在A、B和C三点气体温度分别为TA、TB和TC,求:
(1)D点的温度TD。
(2)矩形对角线交点H处的温度TH。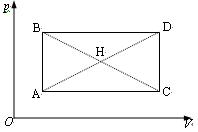
如图所示,轻杆长2L,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动。
(1)若A球在最高点时,杆A端恰好不受力,求此时O轴的受力大小和方向;
(2)若B球到最高点时的速度等于第(1)小问中A球到达最高点时的速度,则B球运动到最高点时,O轴的受力大小和方向又如何?
某宇航员在飞船发射前测得自身连同宇航服等装备共重840N,在火箭发射阶段,发现当飞船随火箭以 的加速度匀加速竖直上升到某位置时(其中g为地面处的重力加速度),其身下体重测试仪的示数为1220N。设地球半径R=6400km,地球表面重力加速度g=10m/s2(求解过程中可能用到
的加速度匀加速竖直上升到某位置时(其中g为地面处的重力加速度),其身下体重测试仪的示数为1220N。设地球半径R=6400km,地球表面重力加速度g=10m/s2(求解过程中可能用到 =1.03,
=1.03, =1.02)。问:
=1.02)。问:
(1)该位置处的重力加速度g′是地面处重力加速度g的多少倍?
(2)该位置距地球表面的高度h为多大?
宇航员在地球表面以一定初速度v0竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度v0竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g=10 m/s2,空气阻力不计)
(1)求该星球表面附近的重力加速度g/;
(2)已知该星球的半径与地球半径之比为R星:R地=1:4,求该星球与地球质量之比M星:M地和两星球第一宇宙速度之比V星:V地