某校高三某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都
受到不同程度的破坏,但可见部分如下,据此解答如下问题: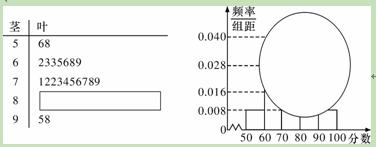
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求分数在[90,100]之间的份数 的数学期望
的数学期望 .
.
一条河的两岸平行,河的宽度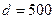 m,一艘船从
m,一艘船从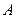 处出发到河对岸.已知船的速度
处出发到河对岸.已知船的速度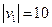 km/h,水流速度
km/h,水流速度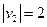 km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论:
km/h.要使船行驶的时间最短,那么船行驶的距离与合速度的比值必须最小.此时我们分三种情况讨论:
(1)当船逆流行驶,与水流成钝角时;
(2)当船顺流行驶,与水流成锐角时;
(3)当船垂直于对岸行驶,与水流成直角时.
请同学们计算上面三种情况,是否当船垂直于对岸行驶时,与水流成直角时,所用时间最短
设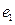 ,
,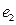 是平面内一组基底,证明:当
是平面内一组基底,证明:当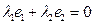 时,恒有
时,恒有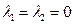 .
.
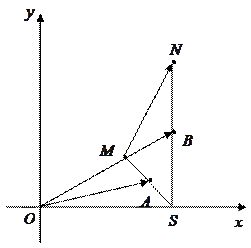
如图,已知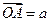 ,
,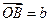 ,任意点
,任意点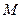 关于点
关于点 的对称点为
的对称点为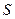 ,点
,点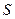 关于点
关于点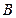 的对称点为
的对称点为 ,用
,用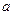 、
、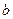 表示向量
表示向量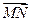 .
.

如图,连接平行四边形 的一个顶点至
的一个顶点至 、
、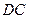 边的中点
边的中点 、
、 ,
,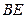 、
、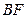 分别与
分别与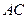 交于
交于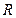 、
、 两点,你能发现
两点,你能发现 、
、 、
、 之间的关系吗?
之间的关系吗?

以初速度 ,抛射角
,抛射角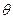 投掷铅球,求铅球上升的最大高度和最大投掷距离.
投掷铅球,求铅球上升的最大高度和最大投掷距离.