如图，四棱锥P－ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正三角形，且平面PDC⊥平面ABCD，E为PC的中点．
(1)求异面直线PA与DE所成的角的余弦值．
(2)求点D到平面PAB的距离．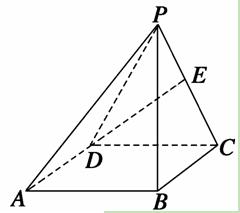
在
中，O为中线AM上一个动点，若AM=2，则
的最小值是_____.
如图, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AA1＝4，点D是AB的中点，（I）求证：（I）AC⊥BC1；
（II）求证：AC 1//平面CDB1；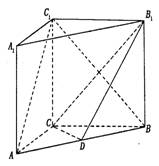
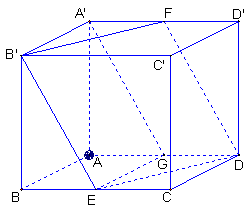
在棱长为a的正方体ABCD—A′B′C′D′中，E、F分别是BC、A′D′的中点
(1)求直线A′C与DE所成的角；
(2)求直线AD与平面B′EDF所成的角；
(3)求面B′EDF与面ABCD所成的角
如图，正三棱柱ABC—A1B1C1的各棱长都相等，D、E分别是CC1和AB1的中点，点F在BC上且满足BF∶FC=1∶3
(1)若M为AB中点，求证
BB1∥平面EFM；
(2)求证EF⊥BC；
(3)求二面角A1—B1D—C1的大小
【挑战自我】
如图，已知PD⊥平面ABCD，AD⊥DC，AD∥BC，PD∶DC∶BC＝1∶1∶
.
（1）求二面角D－PB－C的正切值；
（2）当AD∶BC的值是多少时，能使平面PAB⊥平面PBC？证明你的结论.