(11·肇庆)(本小题满分8分)如图9.一次函数y=x+b的图象经过点B (-1,0),且与反比例函数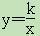 (k为不等于0的常数)的图象在第一象限交于点A (1,n).求:
(k为不等于0的常数)的图象在第一象限交于点A (1,n).求:
(1)一次函数和反比例函数的解析式;
(2)当1≤x≤6时,反比例函数y的取值范围.
一个等腰三角形的周长为 ,一边长为
,一边长为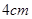 ,求底边上的高.
,求底边上的高.
如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
如图是用硬纸板做成的四个全等的直角三角形,两直角边长分别是 ,斜边长为
,斜边长为 和一个边长为
和一个边长为 的正方形,请你将它们拼成一个能证明勾股定理的图形.
的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图.
(2)证明勾股定理.
某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A、 B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方? 
小明想知道学校旗杆的高度.他测量得旗杆顶端所系的绳子垂到地面还多1米,当他拎着绳子的下端点拉直,并揿在地面上时,此点离开旗杆底部是5米.你能帮助小明计算出旗杆的高度吗?