一个等腰三角形的周长为 ,一边长为
,一边长为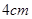 ,求底边上的高.
,求底边上的高.
如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM。
某梁平特产专卖店销售“梁平柚”,已知“梁平柚”的进价为每个10元,现在的售价是每个16元,每天可卖出120个.市场调查反映:如调整价格,每涨价1元,每天要少卖出10个;每降价1元,每天可多卖出30个。
(1)如果专卖店每天要想获得770元的利润,且要尽可能的让利给顾客,那么售价应涨价多少元?
(2)请你帮专卖店老板算一算,如何定价才能使利润最大,并求出此时的最大利润?
“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现万州人追梦的风采,我区某校开展了以“梦想中国,逐梦万州”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
| 等级 |
成绩(用s表示) |
频数 |
频率 |
| A |
90≤s≤100 |
x |
0.08 |
| B |
80≤s<90 |
35 |
y |
| C |
s<80 |
11 |
0.22 |
| 合 计 |
50 |
1 |
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 ,y的值为 。
(2)将本次参赛作品获得A等级的学生一次用A1,A2,A3,…表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率。
先化简,再求值: ,其中x满足方程:x2+x﹣6=0。
,其中x满足方程:x2+x﹣6=0。
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△ .
.
(1)画出△ ,直接写出点
,直接写出点 ,
, 的坐标;
的坐标;
(2)在旋转过程中,点B经过的路径的长;
(3)求在旋转过程中,线段AB所扫过的面积.