(9分)已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且
分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
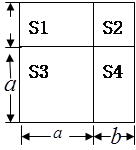
我们可以用几何图形来解释一些代数恒等式,
(1)如图可以用来解释(a+b)2=a2+2ab+b2
(2)请构图解释:(a+2b)2=a2+4ab+ 4b2
|
解方程: .
.
先化简,再求值: .
.
化简或计算
(1)、
(2)、
(3)、 4x3÷(-2x)2
(4)、(x-3)(x-2)-(x+1)2
(5)、a(2a+3)-2(a +3)(a-3)
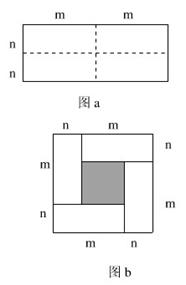
图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
(1)、你认为图b中的阴影部分的正方形的边长等于多少?
(2)、请用两种不同的方法求图b中阴影部分的面积。
方法1:
方法2:
(3)、观察图b你能写出下列三个代数式之间的等量关系吗?
代数式:
(4)、根据(3)题中的等量关系,解决如下问题: ,则
,则 =。(写出过程)
=。(写出过程)