设an=1+q+q2+…+qn-1(n∈N,q≠±1),An=C n1a1+C n2a2+…+Cnnan,求An(用n和q表示).
设集合I={1,2,3,4,5}.选择I的两个非空子集A和B,求使B中最小的数大于A中最大的数的不同选择方法有多少种?
有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有多少种?
已知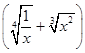 n展开式中的倒数第三项的系数为45,求:
n展开式中的倒数第三项的系数为45,求:
(1)含x3的项;
(2)系数最大的项.
(1)求证:2n+2·3n+5n-4能被25整除;
(2)求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).