为了解七年级学生每周的课外阅读情况，某校语文组调查了该校七年级部分学生某周的课外阅读量（精确到千字），将调查数据经过统计整理后，得到如下频数分布直方图，回答下列问题：
（1）填空：
①该校语文组调查了 名学生的课外阅读量；
②左边第一组的频数＝ ，频率＝ 。
（2）求阅读量在1.1万字以上的人数。
（1）已知数
与
互为相反数，
与
互为倒数，
，求式子
的值．
（2）若
，求
的值．
先化简再求值：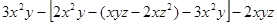
，其中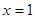
，
，
．
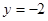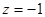在平面直角坐标系xOy中，已知抛物线
与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，sin∠MOH＝
．
（1）求此抛物线的函数表达式；
（2）过H的直线与y轴相交于点P，过O，M两点作直线PH的垂线，垂足分别为E，F，若
时，求点P的坐标；
（3）将（1）中的抛物线沿y轴折叠，使点A落在点D处，连接MD，Q为（1）中的抛物线上的一动点，直线NQ交x轴于点G，当Q点在抛物线上运动时，是否存在点Q，使△ANG 与△ADM相似？若存在，求出所有符合条件的直线QG的解析式；若不存在，请说明理由。
图，△ABC中，点E、P在边AB上，且AE＝BP，过点E、P作BC的平行线，分别交AC于点F、Q．记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3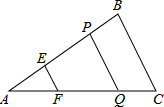
（1）求证：EF＋PQ＝BC
（2）若S1＋S3＝S2，求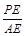
的值
如图，AB是⊙O的直径，延长AB至P，使BP=OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB=α，∠POC=2β．求证：tanα•tanβ=
．