△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连CF
(1)如图,当D点在BC上时,试探索BE与CF的关系,并证明。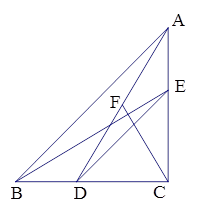
(2)如图,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明;如果不成立,请写出相应的正确的结论并加以证明。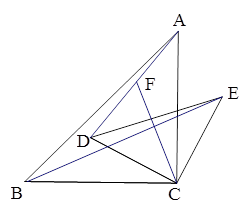
(11分) 某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
根据以上信息,解答下列问题: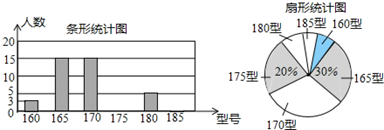
(1)该班共有多少名学生?其中穿175型校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整.
(3)求该班学生所穿校服型号的众数和中位数
如图,一次函数的图象经过A、B两点,与x轴交于点C,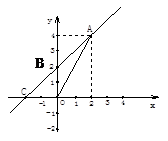
(1)求直线AB的解析式
(2)求△AOC的面积.
已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分EF线分别交AD、BC于点E、F,垂足为O.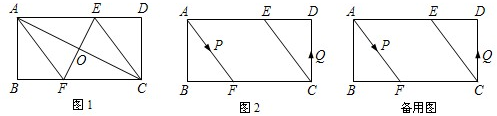
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值。
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.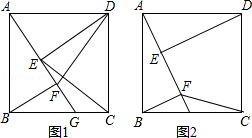
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB=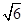 ,G为CB中点,连接CF,直接写出四边形CDEF的面积.
,G为CB中点,连接CF,直接写出四边形CDEF的面积.
如图所示,一根长2.5米的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,此时OB的距离为0.7米,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿地面向右滑行.
(1)如果木棍的顶端A沿墙下滑0.4米,那么木棍的底端B向外移动多少距离?
(2)请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由.