在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.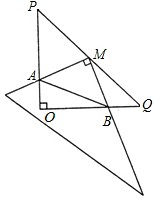
(1)求证:MA=MB;
(2)连接AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
下列图表是某校今年参加中考体育的男生1000米跑、女生800米跑的成绩中分别抽取的10个数据.
| 考生 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 男生 成绩 |
3′05〞 |
3′11〞 |
3′53〞 |
3′10〞 |
3′55〞 |
3′30〞 |
3′25〞 |
3′19〞 |
3′27〞 |
3′55〞 |
(1)求出这10名女生成绩的中位数、众数和极差;
(2)按规定,男生1000米跑成绩不超过3′35〞就可以得满分.该校学生有490人,男生比女生少70人. 请你根据上面抽样的结果,估算该校考生中有多少名男生该项考试得满分?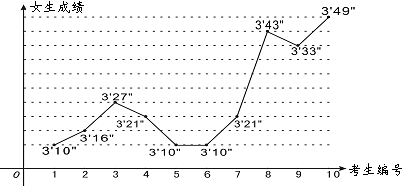
如图,在平面直角坐标系 中,等边
中,等边 中,BC∥
中,BC∥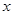 轴,且BC=
轴,且BC=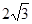 ,顶点A在抛物线
,顶点A在抛物线 上运动.
上运动.
(1)当顶点A运动至与原点重合时,顶点C是否在该抛物线上?
(2)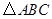 在运动过程中有可能被
在运动过程中有可能被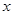 轴分成两部分,当上下两部分的面积之比为1:8(即
轴分成两部分,当上下两部分的面积之比为1:8(即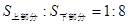 )时,求顶点A的坐标;
)时,求顶点A的坐标;
(3)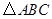 在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
如图1,△ABC内接于半径为4cm的⊙O,AB为直径,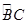 长为
长为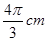 .
.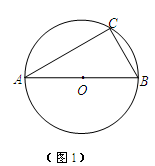
(1)计算∠ABC的度数;
(2)将与△ABC全等的△FED如图2摆放,使两个三角形的对应边DF与AC有一部分重叠,△FED的最长边EF恰好经过 的中点M.求证:AF=AB;
的中点M.求证:AF=AB;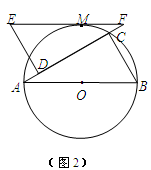
(3)设图2中以A、C、M为顶点的三角形面积为S,求出S的值.
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC.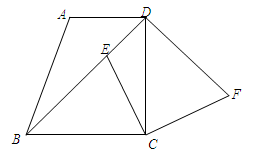
(1)求证:BD⊥DF;
(2)当 时,试判断四边形DECF的形状,并说明理由.
时,试判断四边形DECF的形状,并说明理由.