某校举行文艺节汇演,评出一等奖5个,二等奖10个,三等奖15个,学校决定给获奖的同学发奖品,同一等次的奖品相同,并且只能从下列所列物品中选取一件:
| 品名 |
小提琴 |
运动服 |
笛子 |
舞鞋 |
口琴 |
相册 |
笔记本 |
钢笔 |
| 单价(元) |
120 |
8 |
24 |
22 |
16 |
6 |
5 |
4 |
(1)如果获奖等次越高,奖品单价就越高,那么学校最少要花多少钱买奖品?
(2)学校要求一等奖的奖品单价是二等奖品单价的5倍,二等奖的奖品单价是三等奖品单价的4倍,在总费用不超过1000元的前提下,有几种购买方案?花费最多的一种方案需要多少钱?
已知:在直角坐标平面内,△ABC三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)
(1)在备用图(1)中,画出△ABC向下平移4个单位长度得到△A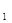 B
B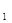 C
C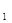 ,点C
,点C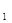 的坐标是________.
的坐标是________.
(2)在备用图(2)中,以点B为位似中心,在网格内画出△A B
B C
C ,使△A
,使△A B
B C
C 与△ABC位似,且位似比为2︰1,点C
与△ABC位似,且位似比为2︰1,点C 的坐标是________.
的坐标是________.
(3)△A B
B C
C 的面积是________平方单位.
的面积是________平方单位.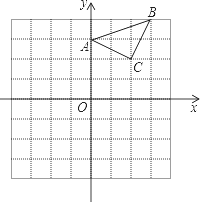
如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.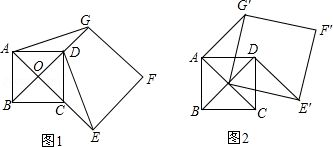
如图,已知,在△ABC中,CA=CB,∠ACB=90°,E,F分别是CA,CB边的三等分点,将△ECF绕点C逆时针旋转α角(0°<α<90°),得到△MCN,连接AM,BN.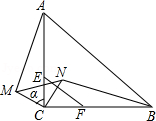
(1)求证:AM=BN;
(2)当MA∥CN时,试求旋转角α的余弦值.
2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍。
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时。试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
在“母亲节”前夕,某花店用16000元购进第一批礼盒鲜花,上市后很快预售一空.根据市场需求情况,该花店又用7500元购进第二批礼盒鲜花.已知第二批所购鲜花的盒数是第一批所购鲜花的 ,且每盒鲜花的进价比第一批的进价少10元.问第二批鲜花每盒的进价是多少元?
,且每盒鲜花的进价比第一批的进价少10元.问第二批鲜花每盒的进价是多少元?