(11·天水)本题共13分(其中第Ⅰ小题6分,第Ⅱ小题7分)
Ⅰ.爱养花的李先生为选择一个合适的时间去参观2011年西安世界园艺博览会,他查阅了
5月10日至16日是(星期一至星期日)每天的参观人数,得到图(1)、图(2)所示的统
计图.其中图(1)是每天参观人数的统计图,图(2)是5月15日(星期六)这一天上午、
中午、下午和晚上四个时段参观人数的扇形统计图,请你根据统计图解答下面的问题:
(1)5月10日至16日这一周中,参观人数最多的是日是_ ▲ ,有_ ▲ 万人,
参观人数最少的是日是_ ▲ ,有_ ▲ 万人,中位数是_ ▲ .
(2)5月15日是(星期六)这一天,上午的参观人数比下午的参观人数多多少人?(精确
到1万人)
(3)如果李先生想尽可能选择参观人数较少的时间参观世园会,你认为选择什么时间较合
适?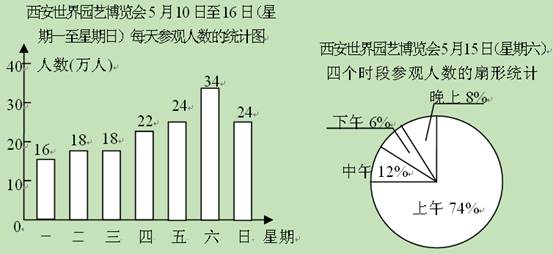
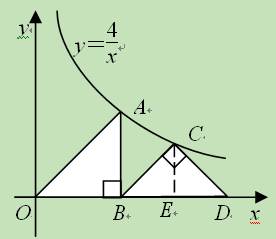
Ⅱ.如图在等腰Rt△OBA和Rt△BCD中,∠OBA=∠BCD=90°,点A和点C都在双曲线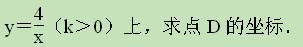
先化简,再求值: ,其中
,其中 满足
满足 .
.
如图,在矩形ABCD中,AC,BD交于点O,若BO=3, ,求矩形ABCD的面积.
,求矩形ABCD的面积.
如图,已知: 为边长是
为边长是 的等边三角形,四边形
的等边三角形,四边形 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边 和正方形
和正方形 按如图①的方式摆放,使点
按如图①的方式摆放,使点 与点
与点 重合,点
重合,点 、
、 、
、 在同一条直线上,
在同一条直线上, 从图①的位置出发,以每秒1个单位长度的速度沿
从图①的位置出发,以每秒1个单位长度的速度沿 方向向右匀速运动,当点
方向向右匀速运动,当点 与点
与点 重合时暂停运动,设
重合时暂停运动,设 的运动时间为
的运动时间为 秒(
秒(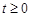 ).
).
(1)在整个运动过程中,设等边 和正方形
和正方形 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)如图②,当点 与点
与点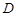 重合时,作
重合时,作 的角平分线
的角平分线 交
交 于点
于点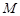 ,将
,将 绕点
绕点 逆时针旋转,使边
逆时针旋转,使边 与边
与边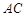 重合,得到
重合,得到 . 在线段
. 在线段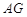 上是否存在
上是否存在 点,使得
点,使得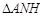 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段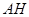 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(3)如图③,若四边形 为边长是
为边长是 的正方形,
的正方形, 的移动速度为每秒
的移动速度为每秒 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.  开始移动的同时,
开始移动的同时, 点从
点从 点开始,沿折线
点开始,沿折线 以每秒
以每秒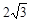 个单位长度开始移动,
个单位长度开始移动, 停止运动时,
停止运动时, 点也停止运动. 设在运动过程中,
点也停止运动. 设在运动过程中,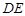 交折线
交折线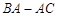 于
于 点,则当
点,则当 时,求
时,求 的值.
的值.
如图,直线AB分别交y轴、x 轴于A、B两点,OA=2, ,抛物线
,抛物线 过A、B两点.
过A、B两点.
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t 取何值时,MN的长度l有最大值?最大值是多少?
如图,梯形ABCD中,AD//BC,E为CD边的中点,F为AD延长线上一点,且满足DF+BF=BC.
(1)若∠A=90º,AD=3,AB=5,BC=9,求BE的长;
(2)求证:BE平分∠FBC.