如图,已知: 为边长是
为边长是 的等边三角形,四边形
的等边三角形,四边形 为边长是6的正方形. 现将等边
为边长是6的正方形. 现将等边 和正方形
和正方形 按如图①的方式摆放,使点
按如图①的方式摆放,使点 与点
与点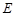 重合,点
重合,点 、
、 、
、 在同一条直线上,
在同一条直线上, 从图①的位置出发,以每秒1个单位长度的速度沿
从图①的位置出发,以每秒1个单位长度的速度沿 方向向右匀速运动,当点
方向向右匀速运动,当点 与点
与点 重合时暂停运动,设
重合时暂停运动,设 的运动时间为
的运动时间为 秒(
秒(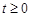 ).
).
(1)在整个运动过程中,设等边 和正方形
和正方形 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)如图②,当点 与点
与点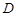 重合时,作
重合时,作 的角平分线
的角平分线 交
交 于点
于点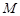 ,将
,将 绕点
绕点 逆时针旋转,使边
逆时针旋转,使边 与边
与边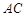 重合,得到
重合,得到 . 在线段
. 在线段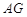 上是否存在
上是否存在 点,使得
点,使得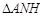 为等腰三角形. 如果存在,求线段
为等腰三角形. 如果存在,求线段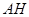 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
(3)如图③,若四边形 为边长是
为边长是 的正方形,
的正方形, 的移动速度为每秒
的移动速度为每秒 个单位长度,其余条件保持不变.
个单位长度,其余条件保持不变.  开始移动的同时,
开始移动的同时, 点从
点从 点开始,沿折线
点开始,沿折线 以每秒
以每秒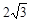 个单位长度开始移动,
个单位长度开始移动, 停止运动时,
停止运动时, 点也停止运动. 设在运动过程中,
点也停止运动. 设在运动过程中,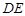 交折线
交折线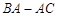 于
于 点,则当
点,则当 时,求
时,求 的值.
的值.
已知平面直角坐标系中有一点M(m-1,2m+3)
(1)当m为何值时,点M到x轴的距离为1?
(2)当m为何值时,点M到y轴的距离为2?
已知,如图,四边形ABCD,∠A=∠B=Rt∠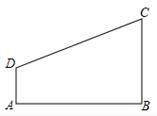
(1)用直尺和圆规,在线段AB上找一点E,使得EC=ED,连接EC,ED(不写作法,保留作图痕迹)
(2)在(1)的图形中,若∠ADE=∠BEC,且CE=3,BC= ,求AD的长.
,求AD的长.
解不等式组: 并把解集在数轴上表示出来。
并把解集在数轴上表示出来。
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: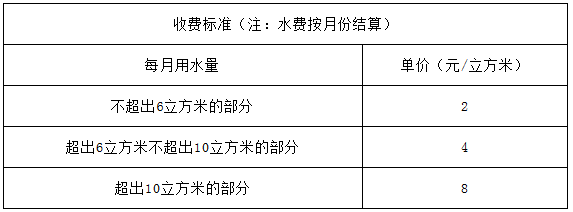
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该户居民5、6两个月共交水费多少元.
如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.