为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：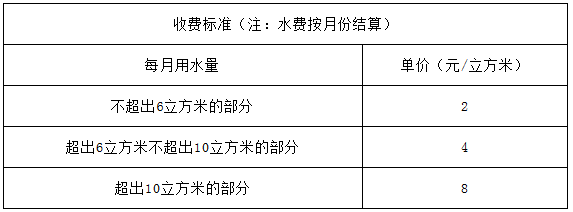
例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8-6）=20（元）．
请根据上表的内容解答下列问题：
（1）若某户居民2月份用水5立方米，则应收水费多少元？
（2）若某户居民3月份交水费36元，则用水量为多少立方米？
（3）若某户居民4月份用水a立方米（其中6＜a＜10），请用含a的代数式表示应收水费．
（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水x立方米，请用含x的代数式表示该户居民5、6两个月共交水费多少元．
如图，将一把两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D、E，量出半径OC=5cm，弦DE=8cm，求直尺的宽度．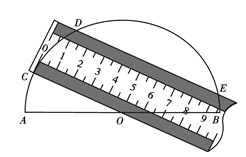
解方程组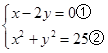
解方程：x(2x－5)=4x－10
在平面直角坐标系中，抛物线
与x轴的两个交点分别为A（-3，0），B（1，0），过顶点C作CH⊥x轴于点H．
（1）a=，b=，顶点C的坐标为．
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由．
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标．
如图，将边长为4的等边三角形AOB放置于平面直角坐标系xOy中，F是AB边上的动点（不与点A，B重合），过点F的反比例函数
（
，
）与OA边交于点E，过点F作FC⊥x轴于点C，连接EF，OF．
（1）若
，求反比例函数的解析式；
（2）在（1）的条件下，试判断以点E为圆心，EA长为半径的圆与
轴的位置关系，并说明理由；
（3）AB边上是否存在点F，使得EF⊥AE？若存在，请求出BF：FA的值；若不存在，请说明理由．