（11·天水）在梯形OABC中，CB∥OA，∠AOC＝60°，∠OAB＝90°，
OC＝2，BC＝4，以点O为原点，OA所在的直线为x轴，建立平面直角坐标系，另有一边
长为2的等边△DEF，DE在x轴上（如图（1）），如果让△DEF以每秒1个单位的速度向
左作匀速直线运动，开始时点D与点A重合，当点D到达坐标原点时运动停止．
（1）设△DEF运动时间为t，△DEF与梯形OABC重叠部分的面积为S，求S关于t的函
数关系式．
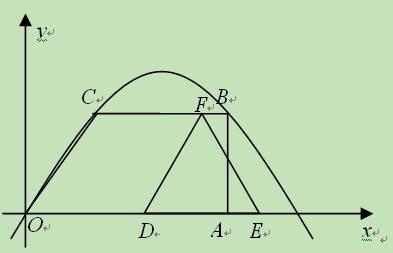
（2）探究：在△DEF运动过程中，如果射线DF交经过O、C、B三点的抛物线于点G，是
否存在这样的时刻t，使得△OAG的面积与梯形OABC的面积相等？若存在，求出t的值；
若不存在，请说明理由．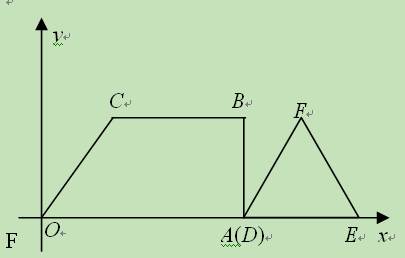
（·辽宁葫芦岛）在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．
（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；
（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，
（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．
（·辽宁沈阳）如图，在平面直角坐标系中，抛物线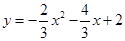
与x轴交于B、C两点（点B在点C的左侧），与y轴交于点A，抛物线的顶点为D．
（1）填空：点A的坐标为（， ），点B的坐标为（， ），点C的坐标为（， ），点D的坐标为（， ）；
（2）点P是线段BC上的动点（点P不与点B、C重合）
①过点P作x轴的垂线交抛物线于点E，若PE=PC，求点E的坐标；
②在①的条件下，点F是坐标轴上的点，且点F到EA和ED的距离相等，请直接写出线段EF的长；
③若点Q是线段AB上的动点（点Q不与点A、B重合），点R是线段AC上的动点（点R不与点A、C重合），请直接写出△PQR周长的最小值．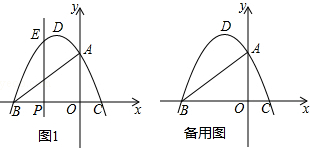
（·辽宁沈阳）如图，在▱ABCD中，AB=6，BC=4，∠B=60°，点E是边AB上的一点，点F是边CD上一点，将▱ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G．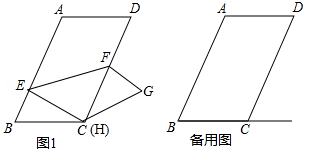
（1）当点H与点C重合时．
①填空：点E到CD的距离是 ；
②求证：△BCE≌△GCF；
③求△CEF的面积；
（2）当点H落在射线BC上，且CH=1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．
（·辽宁沈阳）如图，已知一次函数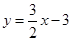
与反比例函数
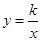的图象相交于点A（4，n），与x轴相交于点B．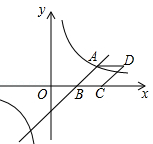
（1）填空：n的值为，k的值为 ；
（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
（3）考察反比函数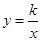的图象，当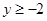
时，请直接写出自变量x的取值范围．
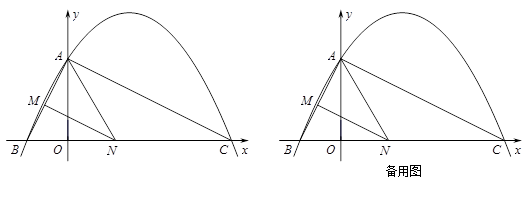
（·辽宁丹东）如图，已知二次函数y= ax2+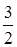
x+c的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．
（1）请直接写出二次函数y= ax2+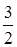x+c的表达式；
（2）判断△ABC的形状，并说明理由；
（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请直接写出此时点N的坐标；
（4）若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．