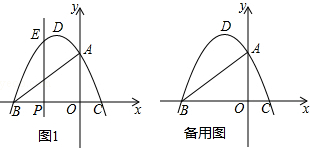
（·辽宁沈阳）如图，在平面直角坐标系中，抛物线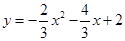与x轴交于B、-优题课

（·辽宁沈阳）如图，在平面直角坐标系中，抛物线与x轴交于B、C两点（点B在点C的左侧），与y轴交于点A，抛物线的顶点为D．
（1）填空：点A的坐标为（，），点B的坐标为（，），点C的坐标为（，），点D的坐标为（，）；
（2）点P是线段BC上的动点（点P不与点B、C重合）
①过点P作x轴的垂线交抛物线于点E，若PE=PC，求点E的坐标；
②在①的条件下，点F是坐标轴上的点，且点F到EA和ED的距离相等，请直接写出线段EF的长；
③若点Q是线段AB上的动点（点Q不与点A、B重合），点R是线段AC上的动点（点R不与点A、C重合），请直接写出△PQR周长的最小值．

科目数学题型解答题难度中等

如图，点 $E$ 在正方形 $ABCD$ 边 $AD$ 上，点 $F$ 是线段 $AB$ 上的动点（不与点 $A$ 重合）， $DF$ 交 $AC$ 于点 $G$ ， $GH ⊥ AD$ 于点 $H$ ， $AB = 1$ ， $DE = \frac{1}{3}$ ．

（1）求 $\tan ∠ ACE$ ；

（2）设 $AF = x$ ， $GH = y$ ，试探究 $y$ 与 $x$ 的函数关系式（写出 $x$ 的取值范围）；

（3）当 $∠ ADF = ∠ ACE$ 时，判断 $EG$ 与 $AC$ 的位置关系并说明理由．

超市购进某种苹果，如果进价增加2元 $/$ 千克要用300元；如果进价减少2元 $/$ 千克，同样数量的苹果只用200元．

（1）求苹果的进价；

（2）如果购进这种苹果不超过100千克，就按原价购进；如果购进苹果超过100千克，超过部分购进价格减少2元 $/$ 千克，写出购进苹果的支出 $y$ （元 $)$ 与购进数量 $x$ （千克）之间的函数关系式；

（3）超市一天购进苹果数量不超过300千克，且购进苹果当天全部销售完，据统计，销售单价 $z$ （元 $/$ 千克）与一天销售数量 $x$ （千克）的关系为 $z = - \frac{1}{100} x + 12$ ．在（2）的条件下，要使超市销售苹果利润 $w$ （元 $)$ 最大，求一天购进苹果数量．（利润 $=$ 销售收入 $-$ 购进支出）

如图， $A$ ， $B$ 是 $⊙ O$ 上两点，且 $AB = OA$ ，连接 $OB$ 并延长到点 $C$ ，使 $BC = OB$ ，连接 $AC$ ．

（1）求证： $AC$ 是 $⊙ O$ 的切线；

（2）点 $D$ ， $E$ 分别是 $AC$ ， $OA$ 的中点， $DE$ 所在直线交 $⊙ O$ 于点 $F$ ， $G$ ， $OA = 4$ ，求 $GF$ 的长．

如图，反比例函数的图象与过点 $A (0, - 1)$ ， $B (4, 1)$ 的直线交于点 $B$ 和 $C$ ．

（1）求直线 $AB$ 和反比例函数的解析式；

（2）已知点 $D (- 1, 0)$ ，直线 $CD$ 与反比例函数图象在第一象限的交点为 $E$ ，直接写出点 $E$ 的坐标，并求 $ΔBCE$ 的面积．

已知关于 $x$ 的一元二次方程 $x^{2} - (2 k + 1) x + k^{2} + k = 0$ ．

（1）求证：无论 $k$ 取何值，方程都有两个不相等的实数根．

（2）如果方程的两个实数根为 $x_{1}$ ， $x_{2}$ ，且 $k$ 与 $\frac{x_{1}}{x_{2}}$ 都为整数，求 $k$ 所有可能的值．

试卷网试题网古诗词网作文网范文网