(本小题满分14分)
已知数列 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, 。
。
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少?
是多少?
(1) 的方程为
的方程为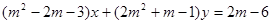 ,根据下列条件分别确定
,根据下列条件分别确定 的值.①
的值.① 轴上的截距是
轴上的截距是 ;②
;② 的倾斜角为
的倾斜角为 ;
;
(2)求经过直线 ,
,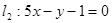 的交点,并且与直线
的交点,并且与直线 垂直的直线方程
垂直的直线方程
已知数列 的前
的前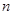 项和为
项和为 ,且
,且 ,设
,设 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前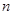 项和
项和 ;
;
(3)设 ,
, ,若数列
,若数列 的前
的前 项和为
项和为 ,求不超过
,求不超过 的最大的整数值.
的最大的整数值.
如图,几何体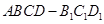 中,四边形
中,四边形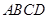 为菱形,
为菱形, ,
,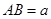 ,面
,面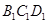 ∥面
∥面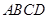 ,
, 、
、 、
、 都垂直于面
都垂直于面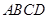 ,且
,且 ,
, 为
为 的中点,
的中点, 为
为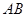 的中点.
的中点.
(1)求证: 为等腰直角三角形;
为等腰直角三角形;
(2)求二面角 的余弦值.
的余弦值.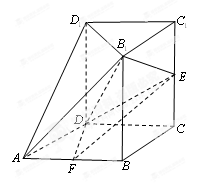
已知函数 ,若存在
,若存在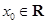 ,使
,使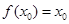 ,则称
,则称 是函数
是函数 的一个不动点.设二次函数
的一个不动点.设二次函数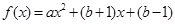 .
.
(1)对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(2)在(1)的条件下,若 的图象上
的图象上 两点的横坐标是
两点的横坐标是 的不动点,且
的不动点,且 两点关于直线
两点关于直线 对称,求
对称,求 的最小值.
的最小值.
已知向量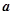
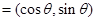 ,
,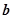
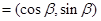 ,且
,且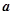 与
与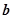 满足
满足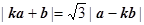 ,其中实数
,其中实数 .
.
(1)试用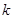 表示
表示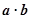 ;
;
(2)求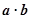 的最小值,并求此时
的最小值,并求此时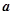 与
与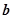 的夹角
的夹角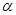 的值.
的值.