（11·大连）（本题11分）如图，在平面直角坐标系中，点A、B、C的坐标分别
为(0，2)、(－1，0)、(4，0)．P是线段OC上的一动点（点P与点O、C不重合），过点P
的直线x＝t与AC相交于点Q
．设四边形ABPQ关于直线x＝t的对称的图形与△QPC重叠
部分的面积为S．
（1）点B关于直线x＝t的对称点B′的坐标为________；
（2）求S与t的函数关系式．
某校为庆祝中国共产党90周年，组织全校1800名学生进行党史知识竞赛．为了解本次知识竞赛成绩的分布情况，从中随机抽取了部分学生的成绩进行统计分析（得分为整数，满分为100分），得到如下统计表：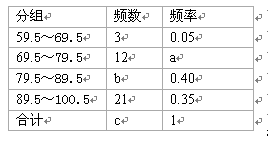
根据统计表提供的信息，回答下列问题：
（1）a＝，b＝，c＝；
（2）上述学生成绩的中位数落在 组范围内；
（3）如果用扇形统计图表示这次抽样成绩，那么成绩在89.5～100.5范围内的扇形的
圆心角为度；
（4）若竞赛成绩80分（含80分）以上的为优秀，请你估计该校本次竞赛成绩优秀的学生
有人．
如图，AC＝AD，∠BAC＝∠BAD，点E在AB上．
（1）你能找出 对全等的三角形；
（2）请写出一对全等三角形，并证明．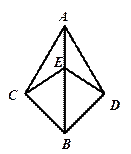
（1）先化简，再求值：x（4－x）＋（x＋1）（x－1），其中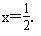
．
（2）解方程：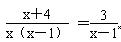
:
（本小题满分14分）已知抛物线y=x2+4x+m（m为常数）
经过点（0,4）.
（1）求m的值；
（2）将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件：它的对称轴（设为直线l2）与平移前的抛物线的对称轴（设为直线l1）关于y轴对称；它所对应的函数的最小值为-8.
①试求平移后的抛物线的解析式；
②试问在平移后的抛物线上是否存在点P，使得以3为半径的圆P既与x轴相切，又与直线l2相交？若存在，请求出点P的坐标，并求
出直线l2
被圆P所截得的弦AB的长度；若不存在，请说明理由.
（本小题满分14分）如图，在边长为8的正方形ABCD
中，点O为AD上一动点（4＜OA＜8），以O为圆心
，OA的长为半径的圆交边CD于点M，连接OM，过点M作圆O的切线交边BC于点N.
（1）求证：△ODM∽△MCN；
（2）设DM=x，求OA的长（用含x的代数式表示）；
（3）在点O运动的过程中，设△CMN的周长为p，试用含x的代数式表示p，你能发现怎样的结论？