(11·兵团维吾尔)甲、乙两县参加由地区教育局举办的“双语口语”大
赛,两县参赛人数相等.比赛结束后,学生成绩分别为7分、8分、9分、10分(满分10分) .甲、
乙两县不完整成绩统计表如右表所示.经计算,乙县的平均分是8.25,中位数是8分.
(1)请写出扇形图中“8分”所在扇形的圆心角度数;求出甲县的平均分、中位数;根据
以上信息分析哪个县的成绩较好;
(2)若地区教育局要组织一个由8人的代表队参加自治区组织的团体赛,为了便于管理,
决定从这两个县的一个县中挑选参赛选手.请你分析该从哪个县选取.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4;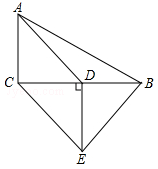
(1)求证:四边形ACED是平行四边形
(2)求四边形ACEB的周长.
如图,直线AC是一次函数y=2x+3的图象,直线BC是一次函数y=﹣2x﹣1的图象.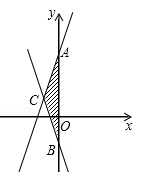
(1)求A、B、C三点的坐标;
(2)求△ABC的面积.
已知y与x+2成正比例,且当x=1时,y=﹣6.
(1)求y与x的函数关系式.
(2)若点(a,2)在此函数图象上,求a的值.
如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且DF=BE.
求证:AE=CF.
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).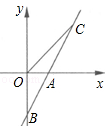
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.