（本小题满分
12分）
在1，2，3，…，9这9个自然数中，任取3个数．
（1）求这3个数中恰有1个偶数的概率；
（2）记X为这3个数中两数相邻的组数，例如：若取出的数为1、2、3，则有两组相邻的数1、2和2、3，此时X的值为2．求随机变量X的颁布列及其数学期望EX．
（本小题满分12分）设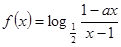
为奇函数，a为常数。
（1）求a的值；
（2）证明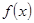
在区间
上为增函数；
（3）若对于区间
上的每一个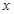
的值，不等式
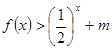恒成立，求实数m的取值范围。
（本小题满分12分）
定义在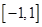
上的偶函数
，已知当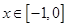
时的解析式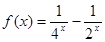
（Ⅰ）写出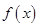
在
上的解析式；
（Ⅱ）求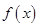在上的最大值.
（本小题满分12分）
直线
与
轴，
轴分别相交于A、B两点，以AB为边做等边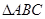
,若平面内有一点
使得
与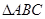的面积相等，求
的值.
（本小题满分12分）如图，在四棱锥
中，平面PAD⊥平面 ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点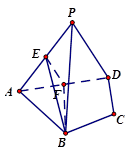
求证：（1）直线EF∥平面PCD；
（2）平面BEF⊥平面PAD
(本小题满分10分)
如图，已知三角形的顶点为A（2， 4），B（0，-2），C（-2，3），
求：
（Ⅰ）AB边上的中线CM所在直线的一般方程；
（Ⅱ）求△ABC的面积.