如图，在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣2，4），过点A作AB⊥y轴，垂足为B，连接OA．
（1）求△OAB的面积；
（2）若抛物线y=﹣x2﹣2x+c经过点A．
①求c的值；
②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围（直接写出答案即可）．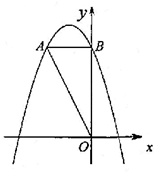
如图所示：工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10cm，测得钢珠顶端离零件表面的距离为8cm，则这个小圆孔的宽口AB的长度为多少？
解方程：①、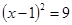
；②、
如图：在等腰梯形ABCD中，AB＝DC＝5，AD＝4，BC＝10．点E在下底边BC上，点F在腰AB上．
①、则梯形的高是；
②、若EF平分等腰梯形ABCD的周长，设BE长为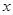
，试用含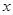的代数式表示△BEF的面积；
③、是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此BE的长；若不存在，请说明理由；
④、是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1︰2的两部分？若存在，求此时BE的长；若不存在，请说明理由．
（1）、动手操作：
如图①：将矩形纸片ABCD折叠，使点D与点B重合，点C落在点
处，折痕为EF，若∠ABE＝20°，那么
的度数为.
（2）、观察发现：
小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．
（3）、实践与运用：
将矩形纸片ABCD按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F重合，展开纸片，此时恰好有MP＝MN＝PQ（如图④），求∠MNF的大小.
我市体育中考规定：可以在立定跳远和一分钟跳绳中任选一项测试，同学们将根据自己平时的运动成绩确定自己的报考项目，下面是小亮同学在近期的两个项目中连续五次测试的得分情况（立定跳远得分统计表和一分钟跳绳的折线图）：
立定跳远得分统计表：
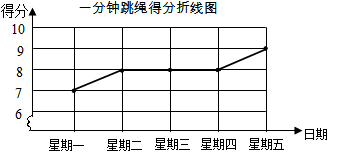
①、请把立定跳远的成绩通过描点并且用虚线在折线图中画出来；
②、请根据以上信息，分别将这两个项目的平均数、极差、方差填入下表：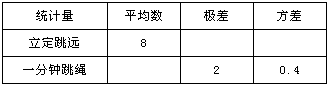
③、根据以上信息，你认为在立定跳远和一分钟跳绳这两个项目中，小亮应选择哪个项目作为体育考试的报考项目？请简述理由．