．(本小题满分14分)已知等比数列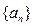
的公比为
，首项为
，其前
项的和为
．数列
的前项的和为
， 数列
的前项的和为
（Ⅰ）若
，
，求
的通项公式；（Ⅱ）①当为奇数时，比较
与
的大小； ②当为偶数时，若
，问是否存在常数
（与n无关），使得等式
恒成立，若存在，求出的值；若不存在，说明理由
（本小题满分10分）
已知动圆
过点
且与直线
相切.
（1）求点的轨迹
的方程；
（2）过点
作一条直线交轨迹于
两点，轨迹在两点处的切线相交于点
，
为线段
的中点，求证：
轴.
D.选修4—5：不等式选讲
(本小题满分10分)
求函数
的最大值．
C．选修4—4：坐标系与参数方程
(本小题满分10分)
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），判断直线和圆的位置关系．
B．选修4—2：矩阵与变换
(本小题满分10分)[
已知矩阵
的一个特征值为3，求另一个特征值及其对应的一个特征向量.
【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答.若多做，则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤．
A.
选修4－1：几何证明选讲
(本小题满分10分)
如图，
与⊙
相切于点
，
为的中点，
过点引割线交⊙于
，
两点，
求证: 
．