（本小题满分12分）如图，已知正方形ABCD和矩形ACEF所在平面互相垂直，
AB=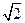
，AF=1，M是线段EF的中点。
(Ⅰ)求证：AM∥平面BDE；
(Ⅱ) 求二面角A－DF－B的大小.
（Ⅲ）试问：在线段AC上是否存在一点P，使得直线PF与AD所成角为60°？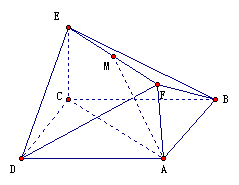
已知数列{an}的各项均为正数，前n项和为Sn，且满足2Sn＝
＋n－4.
(1)求证{an}为等差数列；
(2)求{an}的通项公式．
设数列{an}的前n项和Sn满足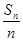
＝3n－2.
(1)求数列{an}的通项公式；
(2)设bn＝
，Tn是数列{bn}的前n项和，求使得Tn<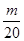
对所有n∈N*都成立的最小正整数m.
已知数列{an}的通项公式为an＝n2－n－30.
(1)求数列的前三项，60是此数列的第几项？
(2)n为何值时，an＝0，an>0，an<0?
(3)该数列前n项和Sn是否存在最值？说明理由．
设数列{an}的前n项和为Sn.已知a1＝a，an＋1＝Sn＋3n，n∈N*.
(1)设bn＝Sn－3n，求数列{bn}的通项公式；
(2)若an＋1≥an，n∈N*，求a的取值范围．
已知数列{an}满足：a1＝1,2n－1an＝an－1(n∈N*，n≥2)．
(1)求数列{an}的通项公式；
(2)这个数列从第几项开始及以后各项均小于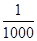
？