如图所示,半径R=0.8m的四分之一光滑圆弧固定在光滑水平面上,轨道上方A点有一质量为m=1.0㎏的小物块;小物块由静止开始下落后打在圆轨道上B点但未反弹,在瞬间碰撞过程中,小物块沿半径方向的分速度立刻减为零,而沿切线方向的分速度不变。此后,小物块将沿圆弧轨道滑下。已知A、B两点到圆心O的距离均为R,与水平方向夹角均为θ=300;C点为圆弧轨道末端,紧靠C点有质量M=3.0㎏的长木板P,木板上表面与圆弧轨道末端切线相平,木板长L=2.5m,取g=10m/s2。
求:(1)小物块刚到达B点时的速度vB;
(2)小物块沿圆轨道到达C点时对轨道的压力;
(3)小物块与长木板的动摩擦因数至少为多大时,小物块才不会滑出长木板。
如图1-2-24所示,甲、乙两辆同型号的轿车,它们外形尺寸如下表所示.正在通过十字路口的甲车正常匀速行驶,车速 ="10" m/s,车头距中心O的距离为20 m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30 m.
="10" m/s,车头距中心O的距离为20 m,就在此时,乙车闯红灯匀速行驶,车头距中心O的距离为30 m.
(1)求乙车的速度在什么范围之内,必定会造成撞车事故.
(2)若乙的速度 ="15" m/s,司机的反应时间为0.5s,为了防止撞车事故发生,乙车刹车的加速度至少要多大?会发生撞车事故吗?
="15" m/s,司机的反应时间为0.5s,为了防止撞车事故发生,乙车刹车的加速度至少要多大?会发生撞车事故吗?
轿车外形尺寸及安全技术参数
| 长l/mm |
宽b/mm |
高h/mm |
最大速度km/h |
急刹车加速度m/s2 |
| 3896 |
1650 |
1465 |
144 |
-4~-6 |
某同学解答如下:
(1)甲车整车经过中心位置,乙车刚好到达中心位置,发生撞车事故的最小速度 ,抓住时间位移关系,有
,抓住时间位移关系,有 ,
, ,故当
,故当 时,必定会造成撞车事故.
时,必定会造成撞车事故.
(2)当 ="15" m/s,为了不发生撞车事故,乙车的停车距离必须小于30m,即
="15" m/s,为了不发生撞车事故,乙车的停车距离必须小于30m,即 ,故
,故 .
.
上述解答过程是否正确或完整?若正确,请说出理由,若不正确请写出正确的解法.
如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求: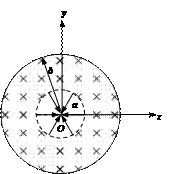
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B。
(3)若磁感应强度取(2)中最小值,且b=(+1)a,要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间。(设粒子与金属球正碰后电量不变且能以原速率原路返回)
如图所示,半径R=0.8m的光滑 圆弧轨道固定在光滑水平面上,轨道上方的A有一个可视为质点的质量m=1kg的小物块,小物块由静止开始下落后打在圆弧轨道的B点,假设在该瞬间碰撞过程中,小物块沿半径方向的分速度立刻减为零,而沿切线方向的分速度不变,此后小物块将沿圆弧轨道下滑,已知A点与轨道圆心O的连线长也为R,且AO连线与水平方向夹角θ=30°,在轨道末端C点紧靠一质量M=3kg的长木板,木板上表面与圆弧轨道末端的切线相平,小物块与长木板间的动摩擦因数μ=0.3,(g取10m/s2)。求:
(1)小物块刚到达B点时的速度大小和方向
(2)要使小物块不画出长木板,木板长度L至少为多少?
如图所示,倾角为θ的光滑绝缘斜面与光滑绝缘水平面连接,整个装置处于水平方向的匀强电场中,在斜面底部有一带电物体B在电场力作用下自静止开始向左匀加速直线运动,与此同时在斜面顶端有一不带电的物体A,自静止开始自由下滑。试求:
(1)物体A到达斜面底端的速度与下滑时间的关系式。
(2)为使A不能追上B,物体B的加速度a的取值范围。(重力加速度g已知)
物体做直线运动,若前一半时间是速度为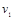 的匀速运动,后一半时间是
的匀速运动,后一半时间是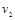 的匀速运动,则整个运动过程的平均速度是?若前一半路程是速度为
的匀速运动,则整个运动过程的平均速度是?若前一半路程是速度为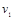 的匀速运动,后一半路程是速度为
的匀速运动,后一半路程是速度为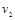 的匀速运动,则整个运动过程的平均速度是?
的匀速运动,则整个运动过程的平均速度是?