(本题满分12分)在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长
(2) 设实数t满足(
设实数t满足( )·
)· =0,
=0, 求t的
求t的 值
值
(本小题满分8分)在直角坐标系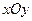 中,直线
中,直线 的参数方程为
的参数方程为
(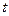 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系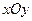 取相同的长度单位,且以原点
取相同的长度单位,且以原点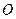 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆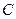 的方程为
的方程为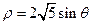 .
.
(I)求圆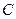 的参数方程;
的参数方程;
(II)设圆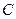 与直线
与直线 交于点
交于点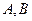 ,求弦长
,求弦长
(本小题满分8分)已知函数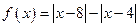 .
.
(Ⅰ)作出函数 的图象;
的图象;
(Ⅱ)解不等式
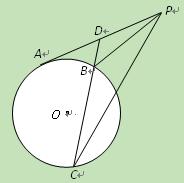
(本小题满分8分)如图, 切⊙O于点
切⊙O于点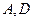 为
为 的中点,过点
的中点,过点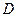 引割线交⊙O于
引割线交⊙O于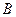 、
、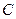 两点.求证:
两点.求证: .
.
(本小题满分8分)直线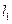 过点
过点 ,且倾斜角为
,且倾斜角为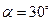 .
.
(I)求直线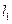 的参数方程;
的参数方程;
(II)若直线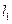 和直线
和直线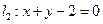 交于点
交于点 ,求
,求 .
.
(本小题满分10分)甲、乙两人进行一次象棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局.
(Ⅰ)求甲获得这次比赛胜利的概率;
(Ⅱ)设ξ表示从第3局开始到比赛结束所进行的局数,求ξ的分布列及数学期望.