为了了 解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如下图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如下图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.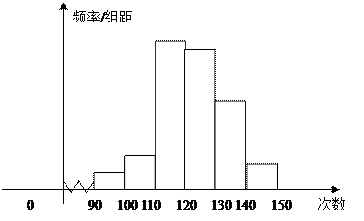
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数 在110以上(含110次)为达标,试估计该学校全体高一的学生达标的概率
在110以上(含110次)为达标,试估计该学校全体高一的学生达标的概率
(3)为了分析学生的体能与身高,体重 等方面的关系,必须再从样本中按分层抽样方法抽出50人作进一步分析,则体能在[120,130)的这段应抽多少人?
等方面的关系,必须再从样本中按分层抽样方法抽出50人作进一步分析,则体能在[120,130)的这段应抽多少人?
(本小题满分12分)设有同频率的两个正弦电流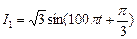 ,
,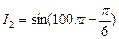 ,把它们合成后,得到电流
,把它们合成后,得到电流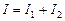 .(1)求电流
.(1)求电流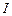 的最小正周期
的最小正周期 和频率
和频率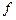 ;(2)设
;(2)设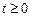 ,求电流
,求电流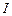 的最大值和最小值,并指出
的最大值和最小值,并指出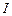 第一次达到最大值和最小值时的
第一次达到最大值和最小值时的 值.
值.
函数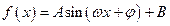
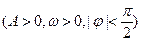 的图像上一个最高点的坐标为
的图像上一个最高点的坐标为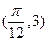 与之相邻的一个最低点的坐标为
与之相邻的一个最低点的坐标为 .
.
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ) 当 ,求函数
,求函数 的单调递增区间和零点.
的单调递增区间和零点.
已知二次函数 的图象过点(0,-3),且
的图象过点(0,-3),且 的解集
的解集 .
.
(Ⅰ)求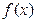 的解析式;
的解析式;
(Ⅱ)求函数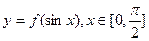 的最值.
的最值.
若x满足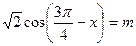
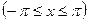 ,为使满足条件的
,为使满足条件的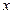 的值(1)存在;(2)有且只有一个;(3)有两个不同的值;(4)有三个不同的值,分别求
的值(1)存在;(2)有且只有一个;(3)有两个不同的值;(4)有三个不同的值,分别求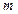 的取值范围.
的取值范围.
已知函数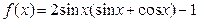 .
.
(1)求函数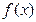 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给定的坐标系内,用五点作图法画出函数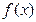 在一个周期内的图象.
在一个周期内的图象.