（本小题满分12分）
如图（1）在Rt△ACB中，∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动，速度为1 cm／s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm／s;连接PQ。若设运动的时间为t(s)(0＜t＜2).根据以上信息，解答下列问题：
（1）当t为何值时，以A、P、Q为顶点的三角形与△ABC相似？
（2）设四边形PQCB的面积为y（
），直接写出y与t之间的函数关系式；
（3）在点P、点Q的移动过程中，如果将△APQ沿其一边所在直线翻折，翻折后的三角形与△APQ组成一个四边形，那么是否存在某一时刻t，使组成的四边形为菱形？若存在，求出t的值；若不存在，请说明理由.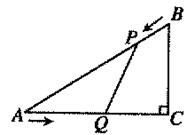
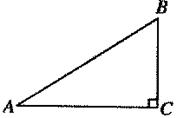
图（1） 备用图 备用图
（本小题满分4分）
如图，在平面直角坐标系中，△ABC和△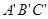
是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2）.
（1）若点A（
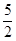，3），则A′的坐标为；（2）若△ABC的面积为m，则△A′B′C′的面积＝.
（本小题满分5分）
如图，□ABCD中，点E在BA的延长线上，连接CE，与AD相交于点F.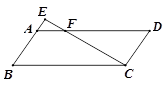
（1）求证：△EBC∽△CDF；
（2）若BC＝8，CD＝3，AE＝1，求AF的长．
（本小题满分5分）
如图，已知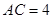
，求AB和BC的长.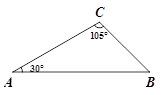
如图，抛物线y =ax2+bx+c过点A（-1，0），且经过直线y =x-3与x轴
的交点B及与y轴的交点C．
（1）求点B、C的坐标；
（2）求抛物线的解析式；
（3）求抛物线的顶点M的坐标；
（4）在直线y =x-3上是否存在点P，使△CMP是等腰三角形？若存在，求出满足条件的P点坐标；若不存在，说明理由．
【初始问题】如图1，已知两个同心圆，直线AD分别交大⊙O于点A、D，交小⊙O于点B、C．AB与CD相等吗？请证明你的结论．
【类比研究】如图2，若两个等边三角形ABC和A1 B1 C1的中心（点Ｏ）相同，且满足AB∥A1B1，BC∥B1C1，AC∥A1C1，可知AB与A1B1，BC与B1C1，AC与A1C1之间的距离相等.直线MQ分别交三角形的边于点M、N、P、Q，与AB所成夹角为∠α（30°＜∠α＜90°）．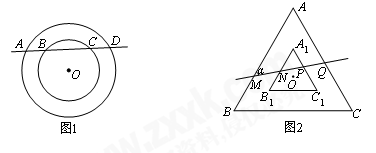
（１）求
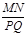（用含∠α的式子表示）；（２）求∠α等于多少度时，MN = PQ．