(9分)已知矩形纸片ABCD中，AB＝2，BC＝3．
操作：将矩形纸片沿EF折叠，使点B落在边CD上．
探究：
(1)如图1，若点B与点D重合，你认为△EDA1和△FDC全等吗？如果全等给出证明，如果不全等请说明理由；
(2)如图2，若点B与CD的中点重合，求△FCB1和△B1DG的周长之比．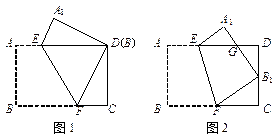
（本题4分）如图，在方格纸中，△ABC的三个顶点和点M都在小方格的顶点上．按要求作图，使△ABC的顶点在方格的顶点上．
（1）过点M做直线AC的平行线；
（2）将△ABC平移，使点M落在平移后的三角形内部．
计算：
（1）x4÷x3·(－3x)2
（2）2x(2y－x) + (x+y)(x－y)
解下列二元一次方程组：
（1）
（2）
如图，长为50cm，宽为
cm的大长方形被分割为8小块，除阴影A、B外，其余6块是形状、大小完全相同的小长方形，其较短一边长为
cm．
（1）从图可知，每个小长方形较长一边长是cm（用含的代数式表示）；
（2）求图中两块阴影A、B的周长和（可以用的代数式表示）；
（3）分别用含，的代数式表示阴影A、B的面积，并求为何值时两块阴影部分的面积相等．
如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动（点P和点C，D不重合，点P，A，B不在同一条直线上），若记∠DAP，∠APB，∠PBC分别为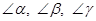
．
（1）当点P在线段CD上运动时，写出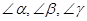
之间的关系并说出理由；
（2）如果点P在线段CD（或DC）的延长线上运动，探究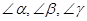之间的关系，并选择其中的一种情况说明理由．