举重运动是力量和技巧充分结合的体育项目,就“抓”举而言,其技术动作可分为预备、提杠发力、下蹲支撑、起立、放下杠铃等动作,如 图所示表示了其中的几个状态。在“提杠发力”阶段,运动员对杠铃施加恒力作用,使杠铃竖直向上加速运动;“下蹲支撑”阶段,运
图所示表示了其中的几个状态。在“提杠发力”阶段,运动员对杠铃施加恒力作用,使杠铃竖直向上加速运动;“下蹲支撑”阶段,运 动员不再用力,杠铃继续向上运动,当运动员处于“下蹲支撑”处时,杠铃的速度恰好为零。
动员不再用力,杠铃继续向上运动,当运动员处于“下蹲支撑”处时,杠铃的速度恰好为零。
(1)为了研究方便,可将“提杠发力”、“下蹲支撑”两个动作简化为较为简单的运动过程来处理,请定性画出相应的速度—时间图像。
(2)已知运动员从开始“提杠发力”到“下蹲支 撑”处的整个过程历时0.8s,杠铃总共升高0.6m,求杠铃获得的最大速度。
撑”处的整个过程历时0.8s,杠铃总共升高0.6m,求杠铃获得的最大速度。
(3)若杠铃的质量为150kg,求运动员提杠发力时对杠铃施加的作用力大小。 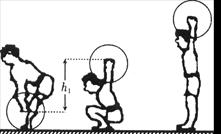

静电喷漆技术具有效率高,浪费少,质量好,有利于工人健康等优点,其装置如图所示.A、B为两块平行金属板,间距d=0.40 m,两板间有方向由B指向A,大小为E=1.0×103 N/C的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的初速度大小均为v0=2.0 m/s,质量m=5.0×10-15 kg、带电量为q=-2.0×10-16 C.微粒的重力和所受空气阻力均不计,油漆微粒最后都落在金属板B上.试求: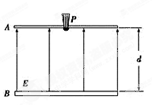
(1)微粒打在B板上的动能;(2)微粒到达B板所需的最短时间;
(3)微粒最后落在B板上所形成的图形及面积的大小.
某兴趣小组对遥控车的性能进行研究。他们让小车在平直轨道上由静止开始运动,并将运动的全过程记录下来并得到v-t图象,如图所示,除2s-10s内的图线为曲线外,其余均为直线,已知小车运动的过程中,2s—14s内小车的功率保持不变,在第14s末关闭动力让小车自由滑行,已知小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变。求:
(1)小车匀速行驶阶段的功率;
(2)小车在第2-10s内位移的大小。
如图所示,一质点做平抛运动先后经过A、B两点,到达A点时速度方向与水平方向的夹角为30°,到达B点时速度方向与水平方向的夹角为60°.
(1)求质点在A、B位置的竖直分速度大小之比;
(2)设质点的位移lAB与水平方向的夹角为θ,求tan θ的值.
质量为m=0.8 kg的砝码悬挂在轻绳PA和PB的结点上并处于静止状态。.PA与竖直方向的夹角37°,PB沿水平方向。质量为M=10kg的木块与PB相连,静止于倾角为37°的斜面上,如图所示。(取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)轻绳PB拉力的大小;
(2)木块所受斜面的摩擦力和弹力大小.
如图所示,将一根光滑的细金属棒折成“V”形,顶角为2θ,其对称轴竖直,在其中一边套上一个质量为m的小金属环P.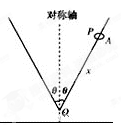
(1)若固定“V”形细金属棒,小金属环P从距离顶点O为x的A点处由静止自由滑下,则小金属环由静止下滑至顶点O需多长时间?
(2)若小金属环P随“V”形细金属棒绕其对称轴以每秒n转匀速转动时,则小金属环离对称轴的距离为多少?