用反证法证明命题：“若a,b∈N，ab能被3整除，那么a,b
中至少有一个能被3整除”时，假设应为（ ）
| A．a、b都能被3整除 | B．a、b都不能被3整除 |
| C．a、b不都能被3整除 | D．a不能被3整除 |
若
，
,则P、Q的大小关系是（）
A． |
B． |
C． |
D．由a的取值确定 |
设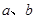
是正数，且a+b=4，则下列各式中正确的一个是（）
A． |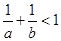
B． |
C． |
D． |
向量
对应的复数是5-4i，向量
对应的复数是-5+4i，则
对应的复数是（）
| A．-10+8i | B．10-8i | C．-8+10i | D．8-10i |
统计中有一个非常有用的统计量
，用它的大小可以确定在多大程度上可以认为“两个分类变量有关系”，下表是反映甲、乙两个班级进行数学考试，按学生考试及格与不及格统计成绩后的2×2列联表.
| 不及格 |
及格 |
总计 |
|
| 甲班 |
12 |
33 |
45 |
| 乙班 |
9 |
36 |
45 |
| 总计 |
21 |
69 |
90 |
则的值为（）
A．0.559 B．0.456C．0.443 D．0.4
设
，且
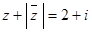，则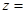
（）
A． |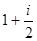
B． |
C． |
D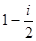． |