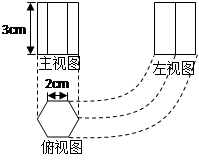如图5,在△ABC和△ADE中,有以下四个论断:① AB=AD,② AC=AE,③ ∠C=∠E,④ BC=DE,请以其中三个论断为条件,余下一个论断为结论,写出一个真命题,并加以证明.
晚上,小亮在广场上乘凉.图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯。
(1)请你在图中画出小亮在照明灯P照射下的影子;
(2)如果灯杆高PO=12m,小亮与灯杆的距离BO=13m,请求出小亮影子的长
度。

如图电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐划一地排列在马路一侧的一
直线上,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都是2 m,已知AB、CD
在灯光下的影长分别为BM =" 1." 6 m,DN =" 0." 6m。
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子。
(2)求标杆EF的影长。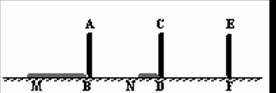
(1)一木杆按如图1所示的方式直立在地面上,请在图中画出它在阳光下的影子(用线段CD表示);
(2)图2是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示),
并在图中画出人在此光源下的影子。(用线段EF表示)。
下图是某几何体的展开图。
(1)这个几何体的名称是;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积。(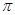 取3.14)
取3.14)
如图所示是某种型号的正六角螺母毛坯的三视图,求它的全面积。